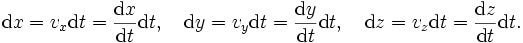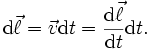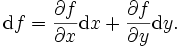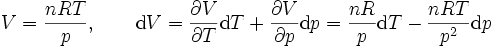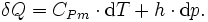Forme différentielle de degré un - Définition

Introduction

En géométrie différentielle, les formes différentielles de degré un, ou 1-formes (différentielles), sont les exemples les plus simples de formes différentielles.

Une 1-forme différentielle sur un ouvert d'un espace vectoriel normé est un champ de formes linéaires c'est-à-dire une application, qui, à un point de l'espace, fait correspondre une forme linéaire. Plus généralement, on peut définir de telles formes linéaires sur une variété différentielle. La définition d'une 1-forme est analogue à celle d'un champ de vecteurs ; ces deux notions sont d'ailleurs en dualité. Pour cette raison, les 1-formes différentielles sont parfois appelées des covecteurs ou champs de covecteurs, en particulier en physique.

L'exemple le plus simple de 1-forme différentielle est la différentielle d'une fonction numérique f, qui se note df. Réciproquement, à partir d'une forme différentielle ω, on peut rechercher s'il existe une fonction primitive de ω, c'est-à dire telle que ω=df. Une condition nécessaire pour l'existence d'une telle fonction f est que la forme différentielle soit fermée. Mais cette condition n'est pas en général suffisante, et le défaut d'existence est relié à la topologie du domaine considéré. Il est mesuré par un élément de ce qui est appelé le premier groupe de cohomologie de De Rham.

Par extension, il est possible de définir des 1-formes différentielles à valeurs dans des espaces vectoriels. Parmi les 1-formes différentielles remarquables, il faut citer les formes de contact et les connexions d'Ehresmann. Toutefois leurs définitions nécessitent une meilleure connaissance des formes différentielles et du calcul différentiel extérieur.

Motivation et premiers exemples

Les accroissements infinitésimaux

Les notations différentielles sont couramment utilisées de façon informelle en sciences physiques, pour désigner l'accroissement très petit d'une variable. Pour une variable réelle, le mot « accroissement » est pris en un sens algébrique, c'est-à-dire qu'un accroissement peut être compté positivement ou négativement. Il est également possible de parler de l'accroissement infinitésimal d'un vecteur variable.

Ainsi, en cinématique, on note x,y,z les variables d'espace, et t la variable de temps, rapportées à un certain référentiel. Les variations infinitésimales correspondantes seront respectivement notées dx,dy,dz,dt. Dans l'étude du mouvement d'un point mobile, donné par des fonctions x(t),y(t),z(t), lors du passage du temps t à un temps infiniment voisin t + dt, les variables d'espace subissent des accroissements donnés par les coordonnées du vecteur vitesse instantanée

On peut également donner l'accroissement vectoriel du vecteur position

Le mode d'introduction choisi cache la nécessité d'introduire les dérivées par un calcul de limite. En effet, même pour des variations très petites, il faudrait introduire un terme d'erreur. Ces formules prennent pourtant un véritable statut mathématique, et sont parfaitement rigoureuses, si on définit correctement les « formes différentielles » .

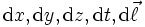
On peut obtenir le déplacement total, c'est-à-dire la variation totale de la fonction position entre deux points a et b (correspondant aux temps t_a et t_b) par un calcul d'intégrale :

.

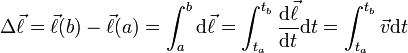
C'est là une propriété générale des formes différentielles : il est possible de les « sommer » le long d'un chemin. Sur cet exemple, cela fournit un calcul de la variation globale d'une fonction.

Différentielles totales

Les problèmes à plusieurs variables font un large emploi des notations différentielles. Quand elle existe, la différentielle d'une fonction f de deux variables x,y s'écrit à l'aide des dérivées partielles :

De nouveau, cette relation s'interprète physiquement, en termes de variations infinitésimales : pour calculer l'accroissement de f, on peut ajouter d'une part l'accroissement infinitésimal de x en considérant y fixé, d'autre part l'accroissement infinitésimal de y en considérant x fixé. On pourrait généraliser à plus de deux variables.

Ainsi, dans la description des systèmes thermodynamiques, les variables et fonctions d'état décrivent l'état d'un système à l'équilibre. Par exemple, pour le gaz parfait, l'équation pV = nRT permet d'exprimer le volume comme fonction de la pression et de la température, puis d'en calculer la différentielle

Lors d'une transformation, l'énergie thermique élémentaire échangée (improprement appelée quantité de chaleur) admet une expression de la forme

C'est une forme différentielle, un objet mathématique de même nature que les exemples précédents, mais qui ne peut pas s'écrire comme la différentielle d'une fonction des variables d'état p,T qui décrivent le système : il n'y a pas de fonction « chaleur », ce qui explique qu'on préfère la notation δQ à dQ.

Les différentielles totales (ou exactes), issues de la différentiation d'une fonction, ne sont donc qu'un cas particulier des formes différentielles de degré 1. Une de leurs propriétés est que l'intégrale d'une forme différentielle exacte le long d'un chemin ne dépend que des extrémités a et b de ce chemin. Traduit en termes de thermodynamique, la variation d'une fonction d'état dépend uniquement des états final et initial du système à l'équilibre.