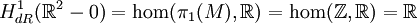Forme différentielle de degré un - Définition

Exactitude

Lorsqu'une forme différentielle ω est la différentielle d'une certaine fonction f, ω est dite exacte et f en est une primitive. Il existe des formes différentielles qui n'ont pas de primitive. Sur un ouvert connexe, lorsqu'une primitive existe, elle est unique à ajout d'une constante près.

Forme différentielle fermée

Sur un ouvert U d'un espace de dimension n, une forme différentielle ω(u) = a₁(u)dx₁ + ... + a_n(u)dx_n est dite fermée lorsque

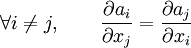
Cette définition est invariante par changement de coordonnées (calcul immédiat). De fait, il est possible de définir les formes différentielles fermées sur une variété de dimension n comme des 1-formes différentielles s'exprimant ainsi dans des cartes locales.

En vertu du théorème de Schwarz, si une forme différentielle est exacte, elle est nécessairement fermée. Le théorème de Poincaré affirme que les deux propriétés sont équivalentes lorsque U est difféomorphe à un ouvert étoilé . Ce théorème de Poincaré se réinterprète en termes de cohomologie (voir ci-dessous).

Ce n'est pas le cas par exemple sur le plan R² privé du point 0 ; ainsi la forme différentielle suivante est fermée sans être exacte :

.

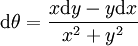
Malgré la notation traditionnelle dθ, cette forme différentielle n'admet pas de primitive. Toutefois, l'exponentielle complexe, donnée en coordonnées réelles par , définit un difféomorphisme local de sur et le tiré en arrière de dθ, qui est tout simplement dv, admet une primitive.

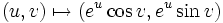
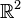
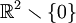
Intégrale curviligne

Soit ω une forme différentielle de degré 1 sur un ouvert U et Γ=([a,b],γ) un arc paramétré tracé sur U. L'intégrale de ω le long de Γ est définie comme

.

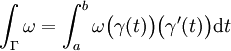
Si on reparamètre Γ en respectant l'orientation, la valeur de cette intégrale est inchangée. On peut donc parler d'intégrale de la forme différentielle le long d'un arc géométrique orienté.

Dans le cadre euclidien, la notion qui correspond à l'intégrale d'une forme différentielle le long d'un arc est la circulation du champ de vecteur associé le long de cet arc.

Mais la définition ci-dessus a l'avantage de ne faire appel à aucune structure supplémentaire (alors que la circulation d'un champ de vecteurs fait intervenir le produit scalaire). Ainsi, cette définition s'étend telle que quand on passe des ouverts de aux variétés : pour tout t, γ'(t) est un vecteur tangent au point γ(t), ω(γ(t)) est une forme linéaire sur l'espace tangent en γ(t), et donc ω(γ(t))(γ'(t)) est un nombre, exactement comme dans le cas des ouverts de l'espace euclidien.

Intégrale et primitives

Si ω est une forme différentielle exacte, de primitive f, son intégrale est donnée par

.

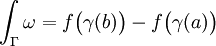
Dans ce cas, l'intégrale ne dépend que des extrémités de l'arc Γ. Notamment, si ce dernier est un arc fermé (γ(b) = γ(a)), l'intégrale est nulle.

En physique, le travail d'une force se calcule par une intégrale curviligne et, dans le cas d'une force conservative, ne dépend pas du chemin parcouru.

Sur une variété M, une 1-forme différentielle est exacte ssi son intégrale curviligne sur tout arc fermé est nulle. Elle est fermée ssi son intégrale sur un arc fermé ne dépend de ce dernier qu'à homotopie près.

Théorèmes de Green et de Stokes

Le théorème de Green concerne les formes différentielles sur un ouvert U du plan. Soit D un domaine compact de U délimité par un arc simple C, positivement orienté et C¹ par morceaux. Soit ω = Pdx + Qdy une 1-forme de classe sur U. Alors

.

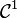
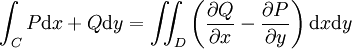
Avec un cadre conceptuel convenable, le théorème peut être généralisé pour un ouvert U d'un espace de dimension plus grande. On obtient alors le théorème de Stokes.

Pour l'énoncer, il faut introduire la dérivée extérieure de ω. C'est une forme différentielle de degré 2, c'est-à-dire un champ de formes bilinéaires antisymétriques sur U. Son expression est donnée par la formule

.

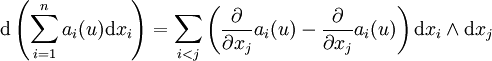
Dans cette expression les 2-formes sont les vecteurs de la base canonique de l'espace des formes bilinéaires antisymétriques sur E. La différentielle extérieure de ω est nulle si et seulement si ω est une forme différentielle fermée.

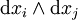
On considère alors une surface S de bord C. Moyennant des hypothèses de régularité et des conventions d'orientation convenables, on obtient le théorème de Stokes :

.

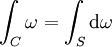
Ce théorème pourrait encore être étendu en considérant des formes différentielles de degré quelconque. Il est nécessaire pour cela d'introduire les concepts généraux d'algèbre extérieure, de différentielle extérieure, d'intégrale d'une forme différentielle.

Premier groupe de cohomologie

Le premier groupe de cohomologie de de Rham est défini comme le quotient de l'espace des 1-formes différentielles fermées par l'espace des 1-formes différentielles exactes. Ce quotient est usuellement noté .

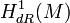
L'ensemble des arcs fermés basés en un point x modulo homotopie forme un groupe pour la concaténation, appelé le groupe fondamental de M, noté . On peut montrer que l'intégration d'une forme différentielle fermée définit un morphisme . Par ce qui précède, ce morphisme est nul si et seulement si la forme différentielle est exacte. On dispose donc d'une application linéaire injective :

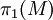
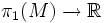
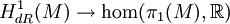
où Hom désigne l'ensemble des morphismes de groupes, ici muni d'une structure naturelle de -espace vectoriel. Cette injection est un isomorphisme.

Par exemple, on a :