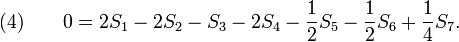Formule BBP - Définition
La liste des auteurs de cet article est disponible ici.
Les records
Pour comparaison, le record actuel de calcul de toutes les décimales de π est de 1 241 milliards de décimales (soit environ 4 123 milliard de chiffres binaires).
- 7 octobre 1996 (Fabrice Bellard) : 400 milliardième chiffre en base 2
- septembre 1997 (Fabrice Bellard) : 1 000 milliardième chiffre en base 2
- février 1999 (Colin Percival) : 40 000 milliardième chiffre en base 2
- 2001 : 4 000 000 milliardième chiffre en base 2
Formules dérivées
Simon Plouffe
Formule originale :
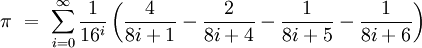
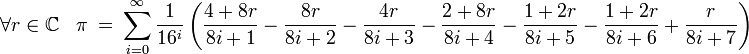
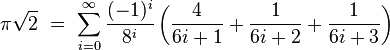
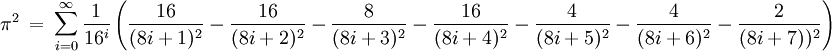
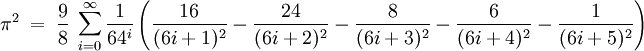
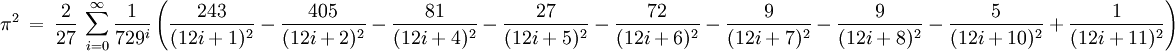
Viktor Adamchick et Stan Wagon (1997)
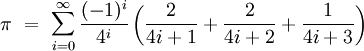
Fabrice Bellard
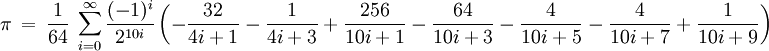
Géry Huvent (2001)
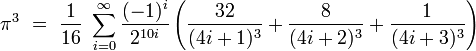
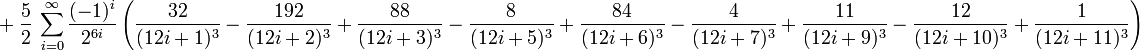
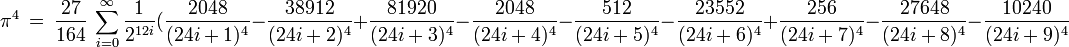
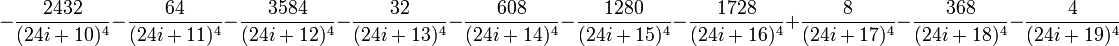
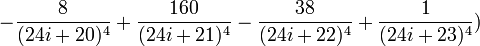
Annexe : démonstration de la formule BBP
Notons
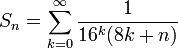
(le cas r = 0 est sa formule originale ; le cas r = − 1 / 4 est, sous une forme plus détaillée, celle d'Adamchick et Wagon).
Posons :
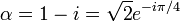
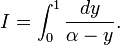
Elle est d'une part reliée aux Sn par
et d'autre part calculable par des méthodes élémentaires (en calculant séparément sa partie réelle et sa partie imaginaire), ou de façon plus synthétique via le logarithme complexe :
L'égalité entre ces deux expressions de I équivaut à :
Mais ln2 s'exprime par ailleurs plus directement en fonction des Sn :
(2) et (3) donnent donc, par soustraction des membres de droite, une relation entre les Sn :
En multipliant le membre de droite de (4) par 1 + 4r et en ajoutant ce produit au membre de droite de (1), on obtient l'égalité (0) annoncée.
Et pour le calcul des décimales ?
Actuellement, aucune formule réellement efficace n'a été découverte pour calculer le ne chiffre de π en base 10. Simon Plouffe a mis au point en décembre 1996, à partir d'une très ancienne série de calcul de π basée sur les coefficients du binôme de Newton, une méthode pour calculer les chiffres en base 10, mais sa complexité en O(n3*log2(n)) la rendait en pratique inutilisable. Fabrice Bellard a bien amélioré l'algorithme pour atteindre une complexité en O(n2), mais cela n'est pas suffisant pour concurrencer les méthodes classiques de calcul de toutes les décimales.
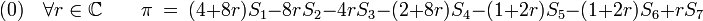
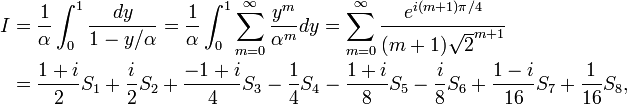
![\begin{align}I&=-\left[\ln(\alpha-y)\right]_0^1=\ln\left(\frac\alpha{\alpha-1}\right)=\ln(1+i)=\ln(\sqrt 2e^{i\pi/4})=\frac{\ln 2}2+i\frac\pi4.\end{align}](https://static.techno-science.net/illustration/Definitions/autres/c/caa4c2f5c0aa21aadd515dd497b78fb7_5738eeffc71783fa58fc0f2c324729bd.png)
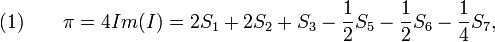
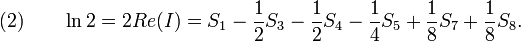
![\begin{align}(3)\quad\ln 2&=[-\ln(2-y^2)]_0^1= \int_0^1\frac{y}{1-y^2/2}dy=\sum_{k\ge 0}\frac 1{(2k+2)2^k}\\&=S_2+\frac 1 2 S_4+\frac 1 4 S_6+\frac 1 8 S_8.\end{align}](https://static.techno-science.net/illustration/Definitions/autres/d/df1f2c22fc2381a0699ac51c30c6e487_8124247d5a44bd8b52ef655bda944241.png)