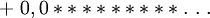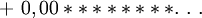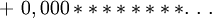Formule BBP - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La formule BBP (ou Bailey-Borwein-Plouffe) permet de calculer l'énième chiffre après la virgule de π en base 2 (ou 16) sans avoir à en calculer les précédents, et en utilisant très peu de mémoire et de temps. Elle a été obtenue le 19 septembre 1995 par Simon Plouffe en collaboration avec David H. Bailey et Peter Borwein.
La formule
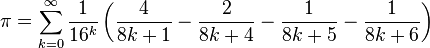
Complexité de cette méthode
Pour calculer le ne chiffre après la virgule de π en base 16 (et donc le 4ne chiffre en base 2):
Complexité temporelle
- Bn'(a) se calcule en temps constant (O(1)). La complexité du calcul de Sn' est donc la même que la complexité du calcul de An'(a).
- An'(a) : en utilisant la méthode d'exponentiation rapide, ses termes se calculent en O(log2(n)) multiplications sur des entiers de taille log2(n). En notant M(k) la complexité de la multiplication de deux entiers de taille k, la complexité est donc O(log(n)M(log(n))). Finalement, la somme des n termes, An'(a), se calcule en temps O(n log(n)M(log(n))). Même en utilisant l'algorithme de multiplication naïf, on obtient une complexité quasi-linéaire de O(n log(n)3).
Complexité spatiale
Le calcul de Bn'(a) s'effectue en espace constant (somme d'un nombre fixé de termes, avec une nombre fixé de chiffres significatifs). Le calcul de An'(a) nécessite d'effectuer des calculs modulo 8k+a, c'est-à-dire de manipuler des nombres de taille log(k) avec k ≤ N. À chaque étape de l'algorithme, on manipule un nombre constant de tels nombres : la complexité en espace du calcul de An'(a) est donc O(log(n)). L'algorithme total utilise donc un espace logarithmique.
Exploitation de la formule pour calculer les chiffres après la virgule de π
Le but est de calculer le Ne chiffre après la virgule de π en base 16.
Déjà, on remarque que le (N+1)e chiffre après la virgule de π en base 16 est la même que le 1re chiffre après la virgule de 16Nπ. En effet, comme en base dix, multiplier un nombre en base 16 par 16 permet de décaler la virgule d'un rang vers la droite. Donc en multipliant un nombre par 16N, la virgule est décalée de N rang vers la droite. Il « suffit » donc de calculer le premier chiffre de 16Nπ, égal par la formule BBP à:
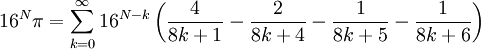
Mais calculer les premiers chiffres derrière la virgule de ce nombre n'est pas si simple, pour deux raisons :
-
- D'abord, ce nombre étant très grand, cela demande d'effectuer des calculs sur des nombres très grands ;
- Ensuite, parce que cette somme est infinie.
Posons
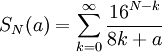
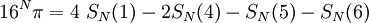
Découpons la somme SN(a) en deux :
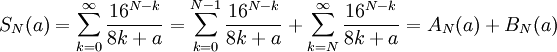
et calculons AN(a) et BN(a) indépendamment.
Calcul de BN(a)
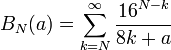
Bien que ce soit une somme infinie, ce terme est très simple à calculer, car on remarque que ses termes deviennent vite très petits et on ne cherche que les premiers chiffres.
- En effet, le premier terme de la somme est :
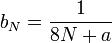
- De plus, chaque terme suivant a un zéro de plus derrière la virgule que le précédent, car pour k ≥ N, bk > 16 bk+1 :
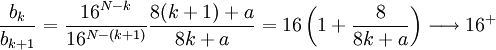
Finalement, la somme BN(a) est de la forme (au pire) :
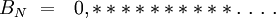
Donc pour obtenir BN(a) avec une précision de P chiffres derrière la virgule, il suffit de calculer les P premiers termes de la somme, plus les quelques suivants pour éviter les problèmes de retenues qui peuvent éventuellement apparaître.
Il suffit donc de calculer :
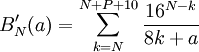
Cette somme n'étant composée que d'un petit nombre de termes (de nombre constant), son temps de calcul est négligeable pour un ordinateur.
Calcul de AN(a)
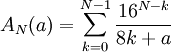
Le problème pour calculer AN(a) est que les premiers termes sont extrêmement grands (N chiffres en base 16 devant la virgule !). Néanmoins, comme on ne cherche que les premiers chiffres derrière la virgule, peu importe la partie entière, aussi grande qu'elle soit. On peut donc s'en « débarrasser » en utilisant arithmétique modulo.
Toute la difficulté se réduit donc à trouver la partie fractionnelle de
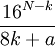
Pour cela, on effectue la division euclidienne de 16N-k par 8k+a :
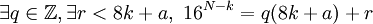
Donc
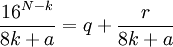
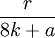
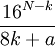
Et
![\frac{r}{8k+a}=\frac{16^{N-k}[8k+a]}{8k+a}](https://static.techno-science.net/illustration/Definitions/autres/c/c7ba6df10acedfe22f71332360cf07f4_fc6143a302ec38cd07679e61b9867ea9.png)
Il suffit donc de calculer :
![A_N'(a)=\sum_{k=0}^{N-1} \frac{16^{N-k}[8k+a]}{8k+a}](https://static.techno-science.net/illustration/Definitions/autres/e/e298893fb43705db131fc81dc092142d_4477cbe15bd87efcd239d896423858ea.png)
En utilisant la méthode d'exponentiation rapide, 16N-k[8k+a] se calcule rapidement (temps d'exécution en O(log2(N-k)).
Conclusion
Au final, pour obtenir les premiers chiffres de π en base 16 (ou 2), il faut calculer les premiers chiffres de :
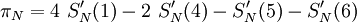
avec
![S_N'(a)=\sum_{k=0}^{N-1} \frac{16^{N-k}[8k+a]}{8k+a}+\sum_{k=N}^{N+P+10} \frac{16^{N-k}}{8k+a}](https://static.techno-science.net/illustration/Definitions/autres/7/7d55a176330f764db1af1e47c92ec441_31911feff0f1ed3f38d9c8a6123ff8e0.png)