Géographie (Ptolémée) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La Géographie ou Manuel de géographie (en grec ancien Γεωγραφικὴ Ὑφήγησις, latinisé en Geographike Hyphegesis, en latin Geographia ou anciennement Cosmographia) est un traité rédigé par Ptolémée vers l'an 150. Cette Introduction géographique à la cartographie est une compilation des connaissances sur la géographie du monde à l’époque de l’empire romain, et dont la redécouverte en Europe au XVe siècle permit de relancer l'étude de la géographie mathématique et de la cartographie.
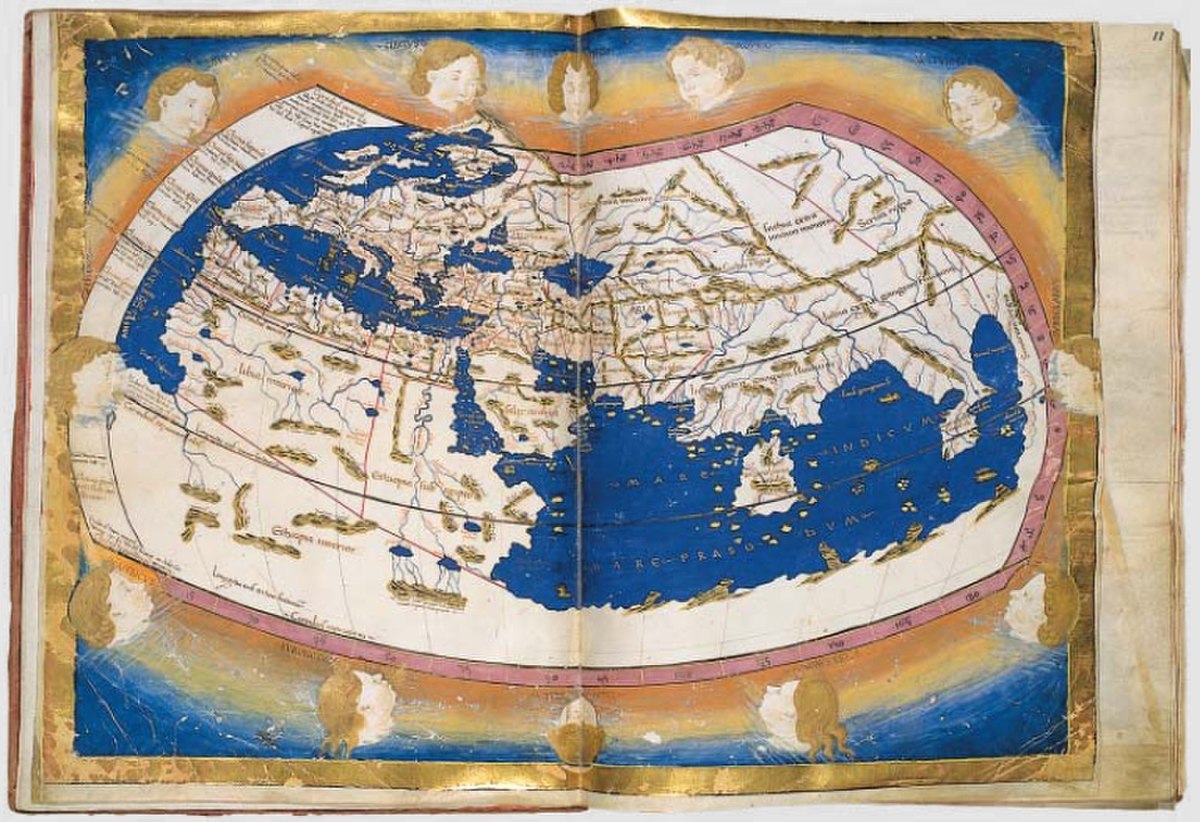
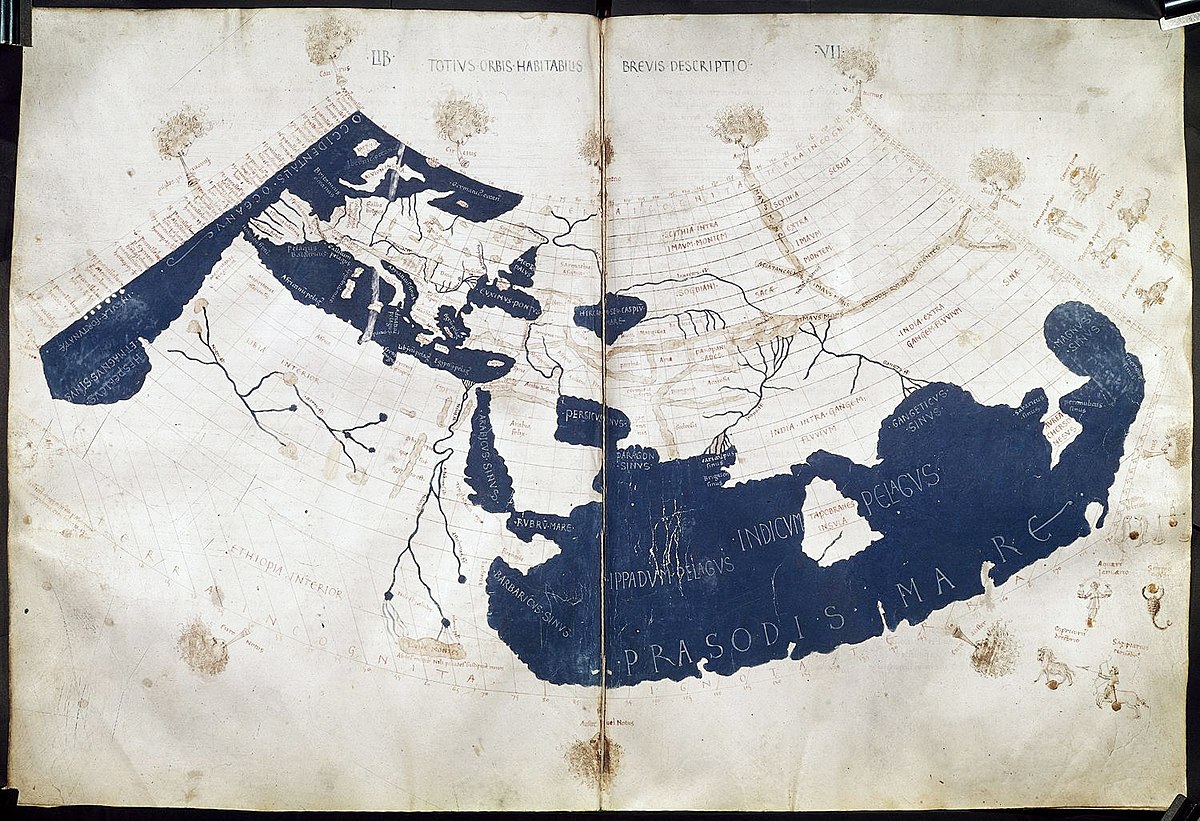
Cet ouvrage est divisé en huit livres. Le premier de ceux-ci expose les bases théoriques du sujet. Les six livres suivants sont consacrés aux diverses parties du monde connu, et contiennent entre autres les coordonnées d'environ 8000 localités. Le huitième et dernier livre, après une brève introduction, utilise les informations contenues dans les livres précédents pour atteindre l'objectif final : dessiner des cartes géographiques de tout le monde habité. Il en contient 27, une carte générale et 26 régions détaillées.
Fondements
Des cartes géographiques basées sur des principes scientifiques et en particulier sur l'utilisation d'une grille de méridiens et de parallèles (c'est-à-dire un système de coordonnées) avaient déjà été réalisées depuis l'époque d'Ératosthène au IIIe siècle av. J.-C.. Au siècle suivant, la géographie mathématique accomplit de grands progrès grâce à Hipparque. À l'époque de l'Empire romain, Marinus de Tyr continue d'approfondir le sujet, et Ptolémée le citera amplement. Tous les ouvrages antérieurs ayant été perdus, il n'est pas facile de juger jusqu'à quel point les méthodes présentées par Ptolémée sont originales, mais il est généralement admis que les principales projections cartographiques décrites dans la Géographie sont de lui. Pour les données relatives aux régions examinées plus en détails, Ptolémée a certainement utilisé, en plus de celles d'Hipparque et de Marinus, les descriptions d'itinéraires et de périples disponibles à son époque.
La théorie présentée dans le premier et le huitième livre
Latitudes et longitudes
Le premier livre de la Géographie présente une analyse des obstacles rencontrés et des méthodes utilisées par Ptolémée. Pour dessiner des cartes géographiques, le premier problème à résoudre était celui du choix des coordonnées, c'est-à-dire les latitudes et les longitudes des lieux à représenter. La latitude, en principe, ne posait pas de difficultés majeures. Diverses méthodes pour la calculer existaient déjà. Ptolémée avait une préférence pour celle utilisant le nombre d'heures maximum de luminosité dans journée. La longitude était beaucoup plus difficile à mesurer. La seule méthode suffisamment précise disponible à cette époque est celle où l'on calcule la différence entre les heures locales d'observation d'une éclipse de Lune. C'est cette méthode, recommandée par Hipparque, qu'a reprise Ptolémée. Ce dernier regrettait cependant d'avoir à sa disposition bien trop peu de chiffres obtenus de cette façon. La plupart du temps, Ptolémée a été contraint de calculer les différences de longitude en se basant , d'une part, sur des estimations des distances linéaires - elle-mêmes tirées d'itinéraires existants - et, d'autre part, sur la longueur du parallèle correspondant. Il avait toutefois remarqué que la différence longitudinale entre deux points placés sur des parallèles différents peut aussi être évaluée si on connait la différence de latitude et l'angle selon lequel elle croise le méridien.
Projections cartographiques
Même en connaissant les coordonnées d'un endroit, le second problème, caractéristique de la cartographie, est de représenter une portion de superficie sphérique sur une surface plane. De toute évidence, il est impossible de le faire sans distorsion. Il faut donc choisir quelles sont les caractéristiques que l'on souhaite conserver intactes lors de la transcription.
Ptolémée décrit deux projections pouvant être utilisées pour réaliser une carte générale de l'écoumène. La première, plus simple, est essentiellement une projection conique dans laquelle les parallèles sont représentés avec des cercles concentriques et les méridiens avec des droites qui convergent vers un même point unique. Ce système tend cependant à représenter les parallèles avec des arcs dont la longueur va en grandissant vers le sud, alors qu'à partir de l'équateur, la longueur réelle diminue. Considérant cette différence inacceptable, Ptolémée a modifié la projection du faisceau placé au sud de l'équateur de la façon suivante : ll a attribué à l'arc qui représente le parallèle le plus au sud (c'est-à-dire le parallèle d'Anti-Meroe, à la latitude 16° 25' S) la même longueur que son symétrique respectif à l'équateur (à la latitude 16° 25' N). Il trace ensuite des méridiens au sud de l'équateur avec des segments qui connectent les points de l'équateur avec ceux du parallèle d'Anti-Meroe placés sur la même longitude.
La deuxième projection, que Ptolémée préférait, est plus complexe. Elle représente les méridiens non pas avec des segments de droite, mais avec des arcs. Le segment du méridien central faisant partie de l'écoumène (90° à l'est des Îles des Bienheureux) est représenté par une ligne verticale sur laquelle les distances sont proportionnelles à la réalité. Sur la prolongation de ce segment, vers le haut, Ptolémée choisit un point C comme centre des parallèles. Il mesure ensuite la circonférence du centre C qui passe par les extrémité du segment et par le point du milieu. À partir de ces trois circonférences, il trace des arcs symétriques au méridien central. Ceux-ci représentent trois parallèles : deux aux extrémités pour marquer les limites de l'écoumène (le parallèle de Thulé au nord, et celui de l'Anti-Meroe au sud) et un troisième à mi-chemin entre les deux. La longueur des arcs est choisie de façon à reproduire les parallèles selon la même échelle que celle utilisée pour le méridien central . Chacun des trois parallèles est divisé en arc égaux pour permettre d'inscrire les longitudes à intervalles de 5 degrés. Les méridiens (tracés tous les 5 degrés) sont ensuite dessinés en forme d'arcs qui passent par les trois points de même longitude sur les trois parallèles spéciaux. Les autres parallèles sont tracés avec des arcs concentriques basés sur les trois précédents, mais les distances représentés par ces nouveaux parallèles ne sont pas proportionnelles à la réalité.
Pour les cartes régionales, Ptolémée, comme il l'explique au début du huitième livre, utilise une troisième projection : la projection cylindrique simple, déjà utilisée par Marinus de Tyr, dans laquelle les méridiens et les parallèles sont représentés par une grille de lignes droites qui se croisent orthogonalement. Ptolémée considérait que les distorsions induites par cette projection la rendaient inutilisable pour une carte générale, mais qu'elles étaient suffisamment limitées dans le cas des cartes régionales.
Les cartes originales de Ptolémée ont été perdues. Il n'est cependant pas difficile de re-dessiner la plupart d'entre elles, grâces aux instructions détaillées de Ptolémée sur les projections utilisées et à la quantité de coordonnées disponibles dans ses manuscrits.