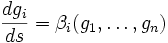Groupe de renormalisation - Définition

Méthodes de renormalisation

« There is no cookbook for the renormalization group »

— K.G.Wilson

Il existe une énorme variété de façons d'implémenter le groupe de renormalisation. En premier lieu, on peut utiliser une approche numérique où on utilise un ordinateur pour garder toutes les constantes de couplage générées par la décimation.

En second lieu, on peut utiliser une approche analytique, perturbative autour d'un point fixe. Parmi les approches perturbatives, on peut mentionner l'approche originale de Wilson d'intégration sur les modes de courte longueur d'onde, les méthodes diagrammatiques issues de la théorie quantique des champs (Brézin, Zinn-Justin, Le Guillou), la renormalisation mutiplicative (Solyom, Fowler, Zawadowski, Di Castro, Jona-Lasinio), les méthodes de gaz de Coulomb (Kosterlitz, Halperin, Nelson, Young), les méthodes de développement de produits d'opérateurs (Cardy).

Enfin, des approches analytiques non-perturbatives ont été développées par A. Houghton et indépendamment par J. Polchinsky. Elles ont trouvé des applications dans la théorie des systèmes désordonnés.

Champs essentiels et inessentiels

Si on suppose maintenant qu'on change les paramètres du hamiltonien H, de sorte que ce hamiltonien s'écrive

H = H * +	∑	giOi
	i

où les O_i sont appelés les « opérateurs » et les g_i sont appelés les « champs ». On peut étudier comment le hamiltonien évolue sous l'action des transformations de renormalisation successives. Pour fixer les idées, imaginons que le groupe de transformations est un groupe continu. Les champs g_i obéissent alors à des équations d'évolution :

Si on veut étudier la stabilité, il suffit de linéariser les fonctions β_i. Après une éventuelle transformation linéaire, les équations d'évolution des champs ont pour solutions :

.

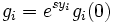
Pour y_i > 0, le champ g_i croit sous l'action des transformations de renormalisation. On dit que g_i est un « champ essentiel » (terminologie de C. Itzykson et J. M. Drouffe) ou « pertinent » (terminologie de N. Boccara). En anglais on parle de « relevant field ».

Pour y_i < 0, le champ g_i decroît sous l'action des transformations de renormalisation. On dit que g_i est un « champ inessentiel » (terminologie de C. Itzykson et J. M. Drouffe) ou « non pertinent » (terminologie de N. Boccara). En anglais on parle de « irrelevant field ».

Pour y_i = 0, le champ g_i ne varie pas à l'ordre linéaire. On parle alors de « champ marginal ». Pour connaitre la stabilité du point fixe il faut aller au-delà de l'ordre linéaire. Pour un champ croissant à l'ordre non linéaire on parlera d'un champ « marginalement essentiel » ou « marginalement pertinent » ( « marginally relevant » en anglais).

Dans la théorie des phénomènes critiques, la température et le champ magnétique sont les seuls champs pertinents au voisinage du point critique. La solution des équations de renormalisation permet de montrer qu'au voisinage du point critique l'énergie libre est de la forme :

F = (T − T_c)^{2 − α}f(H / (T − T_c)^{γ + β})

et satisfait donc l'hypothèse d'homogénéité de Widom. Plus généralement, le groupe de renormalisation permet de prédire l'ensemble des exposants critiques du système en étudiant comment son hamiltonien s'éloigne du hamiltonien de point fixe sous l'action du groupe de renormalisation.