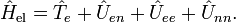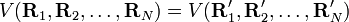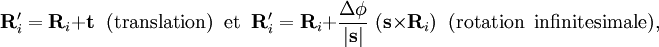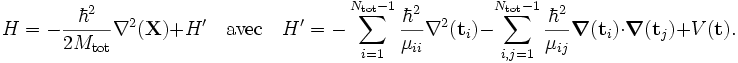Hamiltonien moléculaire - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Introduction - Termes secondaires - Hamiltonien coulombien - Hamiltonien à noyau fixé - Équation de Schrödinger liée au hamiltonien coulombien - Hamiltonien du mouvement nucléaire de Watson - Hamiltonien de mouvement nucléaire harmonique

Hamiltonien à noyau fixé

Le hamiltonien à noyau fixé décrit l'énergie des électrons dans le champ électrostatique des noyaux, où les noyaux sont postulés comme étant stationnaires par rapport à un référentiel galiléen.
La forme du hamiltonien électronique est :

Les coordonnées des électrons et noyaux sont exprimés par rapport au référentiel qui se meut avec les noyaux, ce qui rend les noyaux immobiles par rapport à ce référentiel. Le référentiel reste parallèle à un référentiel fixé dans l'espace. Il s'agit d'un référentiel galiléen car les noyaux sont postulés comme non-accélérés par des forces ou couples externes. L'origine du référentiel est arbitraire, habituellement positionnée sur un noyau central où sur le centre de masse nucléaire. Parfois, il est postulé que les noyaux sont « au repos dans un référentiel fixe ». Ce postulat implique que les noyaux sont des particules classiques, car une particule quantique ne peut être au repos, ce qui signifierait qu'il aurait une quantité de mouvement nulle et une position définie, ce qui contredit le principe d'incertitude d'Heisenberg.
Les positions nucléaires étant constantes, l'opérateur énergie cinétique est invariant par translation selon tout vecteur nucléaire. Le potentiel coulombienne, dépendant des différences vectorielles, est aussi invariant. Dans la description des orbitales atomiques et pour le calcul des intégrales sur les orbitales atomiques, cette invariance est utilisée en dotant tous les atomes de la molécule avec leurs référentiels propres localisés parallèles au référentiel fixe.
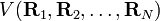
Comme indiqué dans l'article approximation de Born-Oppenheimer, un nombre suffisant de solutions à l'équation de Schrödinger de $H el$ conduit à une surface d'énergie potentielle (SEP) $V(\mathbf{R}_1, \mathbf{R}_2, \ldots, \mathbf{R}_N)$ . Il est postulé que la dépendance fonctionnelle de V sur ses coordonnées est telle que :

pour

où t et s sont des vecteurs arbitraires et Δφ est un angle infinitésimal, Δφ >> Δφ². Cette condition d'invariance sur la SEP est automatiquement remplie lorsque la SEP s'exprime en termes de différences de, et d'angles entre, les R_i,, ce qui est habituellement le cas.

Équation de Schrödinger liée au hamiltonien coulombien

Le hamiltonien coulombien a un spectre continu en raison du mouvement du centre de masse de la molécule dans un espace homogène. En mécanique classique, il est facile de distinguer le mouvement du centre de masse d'un système de masses ponctuelles. Son mouvement est classiquement découplé des autres mouvements. Il se déplace uniformément (avec une vitesse constante) dans l'espace comme s'il était une particule ponctuelle de masse égale à la somme M_tot des masses de toutes les particules.
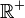
En mécanique quantique, une particule libre possède comme fonction d'état une fonction d'onde plane, qui est une fonction qui n'est pas intégrable quadratiquement d'un moment clairement défini. L'énergie cinétique de cette particule appartient à $\mathbb{R}^+$ . La position du centre de masse est uniformément probable dans tout l'espace, selon le principe d'incertitude de Heisenberg.
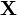
La séparation particulière du mouvement du centre de masse est, en mécanique quantique, beaucoup plus lourde qu'en mécanique classique. en introduicant le vecteur coordonnées du centre de masse $\mathbf{X}$ comme trois des degrés de liberté du système et en éliminant le vecteur coordonnée d'une particule (arbitraire), le nombre total de degrés de liberté restant donc le même, on peut obtenir par transformation linéaire un nouvel ensemble de coordonnées t_i. Ces coordonnées sont des combinaisons linéaires des anciennes coordonnées de toutes les particules (noyaux et électrons). En appliquant le théorème de dérivation des fonctions composées, on peut montrer que :

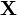
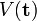
Le premier terme de $H$ est l'énergie cinétique du mouvement du centre de masse, qui peut être traité séparément, $H'$ ne dépendant pas de $\mathbf{X}$ . Comme indiqué plus haut, ses états propres sont des ondes planes. Les constantes 1/μ_ij sont positives et sont des combinaisons linéaires de toutes les masses inversées 1/m_i. Elles constituent les masses réduites généralisées. Le potentiel $V(\mathbf{t})$ rassemble les termes de Coulomb exprimés dans les nouvelles coordonnées. Le premier terme de $H'$ est similaire de manière habituelle à un opérateur énergie cinétique. Le second terme est connu sous l'appellation de terme de polarisation massique. Le hamiltonien invariant par translation $H'$ peut être démontré comme étant auto-adjoint et lié à ce qui suit. Ceci étant dit, sa valeur propre la plus basse est réelle et finie. Bien que $H'$ soit nécessairement invariant par permutations de particules identiques (car $H$ et l'énergie cinétique du centre de masses sont invariants), son invariance n'est pas manifeste.
Peu d'applications moléculaires de $H'$ existent actuellement. On pourra cependant se référer au travail fondamental sur la molécule d'hydrogène pour les premières applications. Dans la grande majorité des calculs de fonctions d'ondes moléculaires le problème électronique est résolu grâce au hamiltonien à noyau fixé provenant de la première étape de l'approximation de Born-Oppenheimer.
On pourra se reporter à la référence pour une discussion approfondie sur les propriétés mathématiques du hamiltonien coulombien. Dans ce papier, est aussi discuté ce qui peut arriver a priori au concept de molécule (comme système stable de noyaux et d'électrons avec une géométrie bien définie) à partir des propriétés du seul hamiltonien coulombien.