Hamiltonien moléculaire - Définition
La liste des auteurs de cet article est disponible ici.
Hamiltonien de mouvement nucléaire harmonique
Dans la suite de cet article, on considèrera la molécule comme semi-rigide. Dans la seconde étape de l'approximation de Born-Oppenheimer, l'énergie cinétique nucléaire Tn est réintroduite et l'équation de Schrödinger avec le hamiltonien :
est alors considérée. On pourra repérer dans sa solution : le mouvement du centre de masse nucléaire (3 degrés de liberté), la rotation globale de la molécule (3 degrés de liberté), et les vibrations nucléaires. En règle générale, ce n'est pas possible de le faire avec l'énergie cinétique nucléaire indiquée, cette dernière ne séparant pas explicitement les six degrés externes de liberté (rotation et translation globales) des 3N-6 degrés de liberté internes. En fait, l'opérateur d'énergie cinétique est ici défini par rapport à un référentiel fixe. Si l'on déplaçait l'origine du référentiel spatial fixe au centre de masse nucléaire, alors, par application de la loi de dérivation des fonctions composées, des termes de polarisation de masse nucléaire apparaitraient. Il est habituel d'ignorer ces termes dans leur globalité, ce qui sera fait par la suite.
Afin de parvenir à une séparation on devra distinguer les coordonnées internes et externes, ce pour quoi Eckart introduisit les conditions à remplir par les coordonnées. On montrera comment ces conditions apparaissent de manière naturelle à partir d'une analyse harmonique dans des coordonnées cartésiennes pondérées par masse.
Afin de simplifier l'expression pour l'énergie cinétique, on introduit les coordonnées pondérées de déplacement :
-
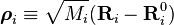
Puisque :
l'opérateur d'énergie cinétique devient :
Si l'on effectue un développement de Taylor de V au voisinage de la géométrie d'équilibre,
et que l'on effectue une troncature après trois termes (c'est-à-dire que l'on effectue une approximation harmonique), on peut décrire V avec seulement le troisième terme. Le terme V0 peut être absorbé dans l'énergie (donnant un nouveau zéro). Le deuxième terme disparaît en raison de la condition d'équilibre. Le terme restant contient la matrice hessienne F de V, qui est symétrique et peut être diagonalisée avec une matrice orthogonale 3N x 3N avec des éléments constants :
Il peut être montré à partir de l'invariance de V par rotation et translation que six des vecteurs propres de F (les six dernières lignes de Q) ont pour valeur propre 0 (sont des modes de fréquence nulle). Ils décrivent l'espace extérieur.
Les premières 3N-6 lignes de Q sont - pour des molécules dans leurs états fondamentaux - des vecteurs propres à valeurs propres non nulles ; elles sont les coordonnées internes et forment une base orthonormée pour un sous-espace de dimension 3N - 6 de l'espace des configurations nucléaires R3N, l'espace interne. Les vecteurs propres de fréquence nulle sont orthogonaux aux vecteurs propres de fréquences non nulles. Il peut être démontré que ces orthogonalités correspondent en fait aux conditions d'Eckart. L'énergie cinétique exprimée dans les coordonnées internes est l'énergie cinétique interne (vibrationnelle).
Avec l'introduction des coordonnées normales :
la partie vibrationnelle (interne) du hamiltonien pour le mouvement nucléaire devient dans l'approximation harmonique
L'équation de Schrödinger correspondante est aisément résolue, en étant factorisée en 3N-6 équations pour des oscillateurs harmoniques mono dimensionnels. La difficulté principale dans cette approximation de la solution de l'équation de Schrödinger du mouvement nucléaire est le calcul du hessien F de V et sa diagonalisation.
Cette approximation du problème du mouvement nucléaire, décrit dans les 3N coordonnées pondérées cartésiennes, est devenu standard en chimie quantique depuis (années 1980-1990) que les algorithmes pour des calculs précis du hessien F sont disponibles. En dehors de l'approximation harmonique, il est problématique que les mouvements externes (rotation et translation) de la molécule ne soient pas considérés. Ils sont pris en compte dans un hamiltonien rovibrationnel qui est parfois appelé hamiltonien de Watson.
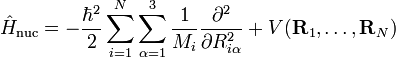
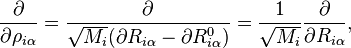
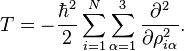
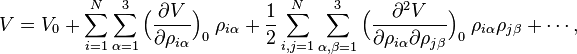
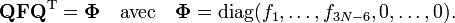
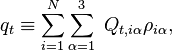
![\hat{H}_\mathrm{nuc} \approx \frac{1}{2} \sum_{t=1}^{3N-6} \left[-\hbar^2 \frac{\partial^2}{\partial q_{t}^2} + f_t q_t^2 \right] .](https://static.techno-science.net/illustration/Definitions/autres/3/30d9b5a62d763b4596dbd352549bef55_7c4445557845137af3371736867f3749.png)

















































