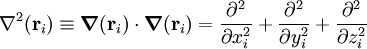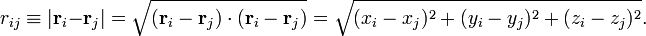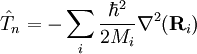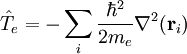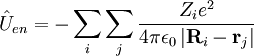Hamiltonien moléculaire - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Introduction - Termes secondaires - Hamiltonien coulombien - Hamiltonien à noyau fixé - Équation de Schrödinger liée au hamiltonien coulombien - Hamiltonien du mouvement nucléaire de Watson - Hamiltonien de mouvement nucléaire harmonique

Termes secondaires

Dans les années 1920 de nombreuses preuves spectroscopiques ont mis en évidence que le hamiltonien coulombien ne prenait pas en compte certains termes, qui bien que plus petits que les énergies cinétiques et coulombiennes, n'en sont pas moins non négligeables. Les observations spectroscopiques ont ainsi conduit à l'introduction d'un nouveau degré de liberté pour les électrons et noyaux, le spin. Ce concept empirique fut doté d'une base théorique par Paul Dirac lorsqu'il introduisit une forme relativiste correcte (invariance de Lorentz) dans l'équation de Schrödinger à une particule. L'équation de Dirac prédit que le spin et le mouvement spatial d'une particule interagissent via un couplage spin-orbite. Par analogie, le couplage spin-autre-orbite fut également introduit. Le fait qu'un spin de particule possède certaines caractéristiques d'un dipôle magnétique conduisit à proposer le couplage spin-spin. D'autres termes sans pendant classique sont : le terme de contact de Fermi (interaction de la densité électronique d'un noyau de taille finie avec un noyau) et le couplage quadrupolaire nucléaire (interaction d'un quadrupôle nucléaire avec le gradient d'un champ électrique dû aux électrons).
Pour finir, un terme de violation de parité prédit par le modèle standard doit également être mentionné. Bien qu'il s'agisse d'une interaction extrêmement faible, elle a attiré l'attention des chercheurs comme le prouve la littérature scientifique car elle dote les énantiomères des molécules chirales d'énergies différentes.

La suite de cet article ignorera les termes de spin et considèrera la solution de l'équation (de Schrödinger dépendante du temps) aux valeurs propres du hamiltonien coulombien.

Hamiltonien coulombien

La forme algébrique de nombreuses observables (c'est-à-dire des opérateurs hermitiques représentant les quantités observables) est obtenue par les règles de quantification suivantes :

écriture de la forme classique de l'observable dans la forme hamiltonienne (comme fonction du moment p et des positions q). Les deux vecteurs sont exprimés dans un référentiel galiléen, habituellement désignéc omme référentiel du laboratoire ou référentiel invariant dans l'espace.
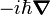
remplacement de p par $-i\hbar\boldsymbol{\nabla}$ et interprétation de q comme un facteur multiplicatif. Ici $\boldsymbol{\nabla}$ est l'opérateur nabla, opérateur vectoriel de dérivation au premier ordre. Les relations de commutations bien connues pour les opérateurs p et q découlent directement des règles de différentiation.

De manière classique, les électrons et les noyaux d'une molécule ont une énergie cinétique de la forme : p²/(2m) et interagissent par les forces de Coulomb, qui sont inversement proportionnelles à la distance r_ij entre la particule i et la particule j.

Dans cette expression r_i désigne le vecteur de coordonnées de n'importe quelle particule (électron ou noyau). À partir d'ici, la lettre majuscule R représentera les coordonnées nucléaires, et la minuscule r les électrons du système. Les coordonnées peuvent être prises dans n'importe quel repère cartésien centré n'importe où dans l'espace, car la distance, comme produit interne, est invariante par rotation du référentiel et, comme norme d'un vecteur différentiel, également invariante par translation dudit référentiel.

En quantifiant l'énergie classique sous forme hamiltonienne on obtien un opérateur hamiltonien moléculaire parfois appelé hamiltonien coulombien. Ce hamiltonien est la somme de cinq classes de termes :

les opérateurs d'énergie cinétique pour chaque noyau du système.
les opérateurs dénergie cinétique pour chaque électron du système.
les opérateurs d'énergie potentielle entre électrons et noyaux - attraction coulombienne totale dans le système.
les opérateurs d'énergie potentielle de répulsions coulombiennes entre électrons.
les opérateurs d'énergie potentielle de répulsions coulombiennes entre noyaux - aussi connue sous le nom d'énergie de répulsion nucléaire. Voir potentiel électrique.

$\hat{T}_n = - \sum_i \frac{\hbar^2}{2 M_i} \nabla^2(\mathbf{R}_i)$
$\hat{T}_e = - \sum_i \frac{\hbar^2}{2 m_e} \nabla^2(\mathbf{r}_i)$
$\hat{U}_{en} = - \sum_i \sum_j \frac{Z_i e^2}{4 \pi \epsilon_0 \left | \mathbf{R}_i - \mathbf{r}_j \right | }$
$\hat{U}_{ee} = {1 \over 2} \sum_i \sum_{j \ne i} \frac{e^2}{4 \pi \epsilon_0 \left | \mathbf{r}_i - \mathbf{r}_j \right | } = \sum_i \sum_{j > i} \frac{e^2}{4 \pi \epsilon_0 \left | \mathbf{r}_i - \mathbf{r}_j \right | }$
$\hat{U}_{nn} = {1 \over 2} \sum_i \sum_{j \ne i} \frac{Z_i Z_j e^2}{4 \pi \epsilon_0 \left | \mathbf{R}_i - \mathbf{R}_j \right | } = \sum_i \sum_{j > i} \frac{Z_i Z_j e^2}{4 \pi \epsilon_0 \left | \mathbf{R}_i - \mathbf{R}_j \right | }.$

M_i est ici la mass du noyau i, Z_i le numéro atomique du noyau i, et m_e la masse de l'électron. L'opérateur laplacien de la particule i est : $\nabla^2(\mathbf{r}_i) \equiv \boldsymbol{\nabla}(\mathbf{r}_i)\cdot \boldsymbol{\nabla}(\mathbf{r}_i) = \frac{\partial^2}{\partial x_i^2} + \frac{\partial^2}{\partial y_i^2} + \frac{\partial^2}{\partial z_i^2}$ . L'opérateur d'énergie cinétique étant un produit interne, il est invariant par rotation dans un repère cartésien par rapport aux x_i, y_i, et z_i exprimés. L'opérateur d'énergie cinétique, cependant, n'est pas invariant par translation (et donc du choix de l'origine du référentiel).