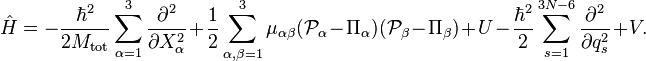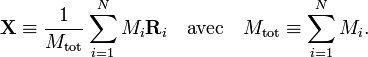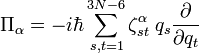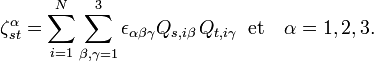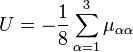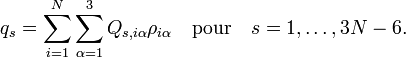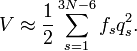Hamiltonien moléculaire - Définition

Hamiltonien du mouvement nucléaire de Watson

Afin d'obtenir un hamiltonien pour les mouvements externes (translation et rotation) couplés aux mouvements internes (vibration), il est usuel de faire un retour à ce niveau à la mécanique classique et de formuler lénergie cinétique classique correspondant à ces mouvements des noyaux. Il est facile de séparer de manière classique le mouvement de translation (du centre de masse) des autres mouvements. Cependant, séparer le mouvement de rotation du mouvement vibrationnel est plus difficile, et en réalité, pas entièrement possible. Cette séparation rovibrationelle fut pour la première fois réalisée par Eckart en 1935 en imposant ce qui est maintenant connu sous le nom de conditions d'Eckart. Lorsque le problème est décrit dans un référentiel (dit d'Eckart) qui tourne avec la molécule, et donc non galiléen, les énergies associées aux forces d'inertie (force centrifuge et force de Coriolis) apparaissent dans l'énergie cinétique.
En général, l'énergie cinétique classique T définit le tenseur métrique g = (g_ij) associé avec les coordonnées curvilignes s = (s_i) par la relation :

.

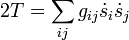
L'étape de quantification est la transformation de cette énergie cintéique classique en un opérateur de chimie quantique. Il est usuel de suivre la méthode proposée par Podolsky en réécrivant l'opérateur de Laplace-Beltrami dans les mêmes coordonnées s (généralisées, curvilignes) utilisées pour la forme classique. L'équation pour cet opérateur nécessite l'inversion du tenseur métrique g et son déterminant. La multiplication de l'opérateur de Laplace-Beltrami par procure l'opérateur d'énergie cinétique quantique requis. Lorsque l'on applique cette méthode aux coordonnées cartésiennes, qui ont une métrique unitaire, la même énergie cinétique est obtenue par application des règles de quantification.
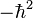
Le hamiltonien de mouvement nucléaire a été décrit par Wilson et Howar en 1936, qui suivirent cette méthode, puis il fut redéfini plus tard par Darling et Dennison en 1940. Cette méthode resta le standard jursqu'en 1968, lorsque Watson fut capable de le simpflier de manière drastique en commutant par les dérivées le déterminant du tenseur métrique. On donnera par la suite le hamiltonien rovibrationnel obtenu par Watson, parfois appelé hamiltonien de Watson. On se doit de préciser que la dérivation de ce Hamiltonien est aussi possible en commençant depuis l'opérateur laplacien dans sa forme cartésienne, en appliquant les transformations de coordonnées, puis en utilisant les règles des dérivation des fonctions composées. Le hamiltonien de Watson, décrivant tous les mouvements des N noyaux, est :

Le premier terme est celui du centre de masse

Le second terme est le terme rotationnel semblable à l'énergie cinétique du rotateur rigide. Ici, est la composante α de l' opérateur de moment angulaire du rotateur rigide fixe. L'opérateur est une composante de l'opérateur dconnu sous le nom d'opérateur de moment angulaire vibrationnel (bien qu'il ne satisfasse pas aux relations de commutation du moment angulaire),

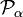
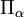
avec la constante de couplage de Coriolis :

Ici, ε_αβγ est le symbole de Levi-Civita. Les termes quadratiques dans sont des termes centrifuges, les termes bilinéaires dans et sont des termes de Coriolis.
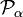
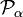
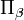
Les quantités Q _{s, iγ} sont des composantes des coordonnées normales introduites ci-dessus. Les coordonnées normales peuvent être introduites de manière alternative par l'application de la méthode GF de Wilson. La matrice symétrique 3 x 3 est appelée tenseur effectif réciproque d'inertie. Si tous les q_s étaient nuls (molécule rigide), le référentiel d'Eckart coinciderait avec le repère des axes principaux (voir rotateur rigide) et serait diagonale, avec les moments d'inertie réciproques d'équilibre sur la diagonale. Si tous les q_s étaient nuls, seule les énergies cinétiques de translation et de rotation rigide seraient exprimées.
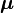
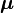
Le terme U de type potentiel est le terme de Watson :

proportionnel à la trace du tenseur effectif réciproque d'inertie. Le quatrième terme dans le hamiltonien de Watson est l'énergie cinétique associée aux vibrations atomiques (nucléaires) exprimée en coordonnées normales q_s, qui comme indiqué ci-dessus, sont données en termes de déplacements nucléaires ρ_iα par :

Enfin, V est l'énergie potentiel non développée par définition dépendante des seules coordonnées internes. Dans l'approximation harmonique, elle prend la forme :