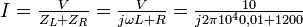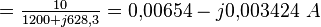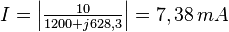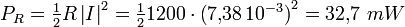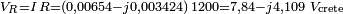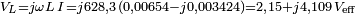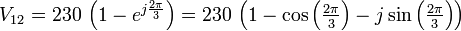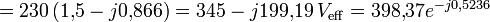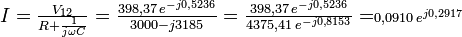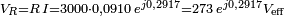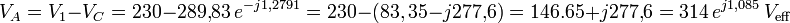Vendredi 2 Mai 2025
Rechercher 🔍

Impédance (électricité) - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Définitions - Diagramme de Fresnel - Sources de tension ou de courant déphasées - Interprétation des résultats - Calcul de circuits avec les impédances - Quand les impédances ne sont pas directement utilisables - Exemples - Origine des impédances

Exemples

Une seule source

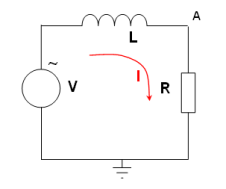
Inductance et résistance en série alimentées par une source sinusoïdale.

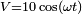
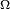
Dans le diagramme de droite nous avons une source sinusoïdale \scriptstyle{V=10\cos(\omega t)} de 10 volts d'amplitude et de 10 kHz de fréquence. En série nous avons une inductance de 10 mH et une résistance de 1,2 k \scriptstyle{\Omega} .
Calculons le courant \scriptstyle{I} qui circule dans le circuit :

I =\textstyle{{V\over Z_L + Z_R}={V\over j\omega L + R}={10\over j2\pi 10^4 0,01 + 1200} }
\textstyle{={10\over 1200 + j628,3}}=0{,}00654-j0{,}003424\,\, A

Le module de ce courant sera :

I =\left|\textstyle{{10\over 1200 + j628,3}}\right|=7,38\,mA

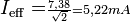
Comme la tension était en valeur crête (amplitude), le courant obtenu l'est aussi. Le courant efficace est I_\mathrm{eff}=\scriptstyle{{7,38\over\sqrt{2} }}=5,22 mA
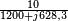
La phase du courant est l'argument du nombre complexe : \scriptstyle{{10\over 1200 + j628,3}}  :

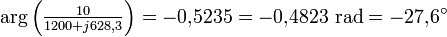
\mathrm{arg}\left(\textstyle{{10\over 1200 + j628,3}}\right)= -0{,}5235 = -0{,}4823 \,\, \mathrm{rad} = -27{,}6^\circ .

Le courant est en retard de phase par rapport à la tension d'alimentation. Ceci est logique puisque le circuit est inductif.

Diagramme de Fresnel d'une bobine et une résistance en série. Le cercle en gris ne sert que comme aide au dessin de l'angle droit entre la tension sur la résistance et l'inductance.

Seule la résistance dissipe de la puissance :

P_R= \textstyle{1\over 2}R\left|I\right|^2=\textstyle{1\over 2}1200\cdot\left(7{,}38\,10^{-3}\right)^2=32{,}7\,\,mW

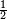
Le \scriptstyle{1\over2} apparaît parce que la valeur du courant utilisée est la valeur crête.

La tension aux bornes de la résistance est :

\scriptstyle{V_R=I\,R=(0{,}00654-j0{,}003424)\,1200=7{,}84-j4{,}109 \,\,V_\mathrm{crete}}

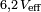
La tension efficace que l'on lirait sur un voltmètre serait le module de cette tension, divisé par racine de 2 : \scriptstyle{6{,}2\, V_\mathrm{eff}}

La tension aux bornes de l'inductance est :

\scriptstyle{V_L=j\omega L\,I\,=j628{,}3\,(0{,}00654-j0{,}003424)= 2{,}15+j4{,}109\, V_\mathrm{eff}}

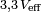
La tension efficace lue avec un voltmètre serait : \scriptstyle{3,3\, V_\mathrm{eff} }

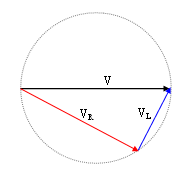
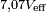
On peut constater que l'addition de deux tensions « complexes » donne bien (aux arrondis près) la tension d'alimentation. Par contre, l'addition de deux tensions lues avec le voltmètre donne une tension plus élevée que celle de l'alimentation ( \scriptstyle{7,07 V_\mathrm{eff}} ). C'est le résultat typique des mesures faites avec un voltmètre sur des circuits dont les tensions ne sont pas en phase.

Deux sources déphasées

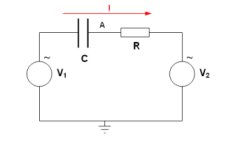
Condensateur et résistance en série entre deux sources sinusoïdales déphasées.

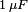
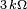
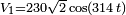
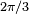
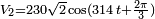
Dans le circuit de droite, un condensateur de \scriptstyle{1\,\mu F} et une résistance \scriptstyle{3\,k\Omega} en série, sont branchés entre deux sources sinusoïdales. Nous prenons comme sources deux phases du réseau triphasé. La source de gauche sera notre source de référence. \scriptstyle{V_1=230\sqrt{2}\cos(314\,t)} . celle de droite est en avance de phase de \scriptstyle{2\pi/3} . Donc \scriptstyle{V_2=230\sqrt{2}\cos(314\,t + {2\pi\over 3})} . 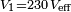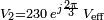Avec le formalisme d'impédances, la source de gauche s'écrira \scriptstyle{V_1=230\,V_\mathrm{eff}} et la source de droite s'écrira \scriptstyle{V_2=230\,e^{j{2\pi\over 3}}\,V_\mathrm{eff}} .

Commençons par calculer la différence de tension entre les deux sources :

\textstyle{V_{12}=230\,\left(1- e^{j{2\pi\over 3}}\right) =230\,\left(1-\cos\left(\textstyle{{2\pi\over 3}}\right)-j\sin\left(\textstyle{{2\pi\over 3}}\right)\right)}\,
\textstyle{=230\,(1{,}5-j0{,}866)=345-j199{,}19\, V_\mathrm{eff}=398{,}37 e^{-j0{,}5236}}\,

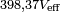
Le module de cette tension est \scriptstyle{398{,}37 V_\mathrm{eff}} , et elle est en retard de 0,5236 radians (30°) par rapport à la tension de référence.

Diagramme de Fresnel correspondant au deuxième exemple. Le premier cercle sert de guide pour les tensions de deux sources. Le second pour l'angle droit entre la tension du condensateur et celle de la résistance.

Le courant qui circule est :

\textstyle{I = {V_{12}\over R +\scriptstyle{1\over j\omega C}} = {398{,}37\,e^{-j0{,}5236}\over {3000 - j3185}}= {398{,}37\, e^{-j0{,}5236}\over 4375{,}41\, e^{-j0{,}8153}}= \scriptstyle{0{,}0910}\, e^{j0{,}2917}}

Comme les valeurs de départ étaient des valeurs efficaces, le courant aussi est une valeur efficace de 91 mA et en avance de phase de 16,71° par rapport à la tension de référence.

La tension aux bornes de la résistance est :

\scriptstyle{V_R=R\,I=3000\cdot 0{,}0910\, e^{j0{,}2917}=273\, e^{j0{,}2917}V_\mathrm{eff} }

La tension aux bornes du condensateur est :

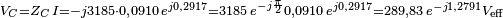
\scriptstyle{V_C=Z_C\,I=-j3185\cdot 0{,}0910\, e^{j0{,}2917}=3185\, e^{-j{\pi\over 2}}0{,}0910\, e^{j0{,}2917}=289{,}83\, e^{-j1{,}2791}V_\mathrm{eff} } .

La tension aux bornes du condensateur est en retard de phase de 73,3° par rapport à la tension de référence. Comme précédemment, l'addition des modules des tensions (celles que l'on mesurerait avec un voltmètre) sur la résistance et le condensateur (563 V) est supérieure à la tension appliquée (398 V).

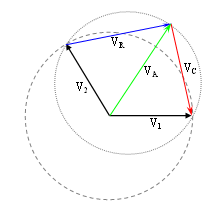
La tension au point A du circuit sera :

V_A= V_1-V_C=230 -289{,}83\, e^{-j1{,}2791}= 230 - (83,35-j277{,}6)=146.65+j277{,}6 = 314\,e^{j1{,}085} \,V_\mathrm{eff}

La tension au point A est plus élevée que la tension de chacune des sources.

Quand les impédances ne sont pas directement utilisables
Origine des impédances
- Introduction - Définitions - Diagramme de Fresnel - Sources de tension ou de courant déphasées - Interprétation des résultats - Calcul de circuits avec les impédances - Quand les impédances ne sont pas directement utilisables - Exemples - Origine des impédances
miniature
Une éruption volcanique en 2018 responsable d'une explosion de vie 🌋
miniature
Un système d'exploitation pour les ordinateurs quantiques voit le jour 🖥️
miniature
Des singularités temporelles dans l'Univers ? 🕰️
miniature
Des fossiles de dinosaures mieux datés 🦖
miniature
Une gigantesque muraille de 10 milliards d'années-lumière dans l'Univers 🔭
miniature
Benchmark: les processeurs quantiques sous la loupe, quels sont les meilleurs ? 🏆
miniature
Découverte d'une "fourmi de l'enfer" vieille de 113 millions d'années 🐜
miniature
Le rôle méconnu de la décharge dans l'usure des batteries 🔋
miniature
1
La fonte des glaces déplace les pôles: quelles conséquences ? 🌍
miniature
L'appareil photo de votre smartphone peut détecter l'antimatière 📱
miniature
Cette étoile-zombie peut déformer les atomes à distance, et elle fonce dans notre galaxie ⭐
miniature
Un mosasaure géant découvert dans le Mississippi 🦕
miniature
Problème, les galaxies meurent plus tôt que prévu 🌀
miniature
Ce lien entre cannabis et troubles psychotiques 🧠
miniature
Une révolution dans le refroidissement des puces électroniques ? 🔥
miniature
Des parasites sous-marins filmés en train de vampiriser un poisson des abysses 👀
miniature
Lucy survole un astéroïde en forme de cacahuète 🚀
miniature
Découverte du fossile d'un dinosaure géant méconnu 🦕
miniature
Mars avait-elle un champ magnétique unilatéral ? 🔍
miniature
Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇
miniature
Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁
miniature
L'électroluminescence du graphène, une découverte inattendue ! 💡
miniature
Cet objet métallique n'a pas été fabriqué sur Terre 🔧
miniature
1
Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡
miniature
Cette super-Terre brûle les attentes des astronomes 🔥
miniature
Découverte exceptionnelle de fossiles d'amphibiens géants 🐸
miniature
Voici ce qui a causé les toutes premières inégalités de richesse 💰
miniature
Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊
miniature
Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭
miniature
Des cellules solaires flexibles battent des records d'efficacité ⚡
miniature
Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀
miniature
Record établi pour un transistor en diamant 💎
miniature
Les sursauts radio rapides trahissent enfin leur origine cosmique 📡
miniature
Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠
miniature
Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊
miniature
Les oscillations collectives des foules humaines denses 🔁
miniature
Une forme inconnue de la matière détectée au LHC ? ⚛️
miniature
Le sel, un facteur méconnu de l'obésité ? 🧂
miniature
L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀
miniature
Découverte tectonique majeure sous les Petites Antilles 🌍
miniature
1
Peut-on geler en chauffant ? ❄️
miniature
Une peau électronique pour doter les robots du sens du toucher 👌
miniature
Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳
miniature
Le cancer inscrit dans nos gènes dès la naissance ? 🧬
miniature
Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥
miniature
Le passé verdoyant du plus grand désert du monde 🐪
miniature
Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷
miniature
Des puces quantiques plus proches que jamais ⚡
miniature
1
Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬
miniature
En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊
Page générée en 0.111 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise