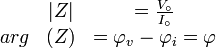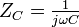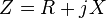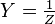Impédance (électricité) - Définition

Introduction

L'impédance électrique mesure l'opposition d'un circuit électrique au passage d'un courant alternatif sinusoïdal. La définition d'impédance est une généralisation de la loi d'Ohm dans l'étude des circuits en courant alternatif.

Le mot impédance fut inventé par Oliver Heaviside en juillet 1886. Il vient du verbe anglais to impede signifiant "retenir", "faire obstacle à" ; verbe qui dérive lui-même du latin impedire qui veut dire "entraver".

Dans un circuit formé par des résistances, condensateurs et bobines, toutes les tensions et les courants sont solutions d'équations différentielles. Mais, si toutes les sources délivrent des courants et des tensions fonctions sinusoïdales du temps de même fréquence et d'amplitude constante, les solutions, à l'état stationnaire (quand tous les phénomènes transitoires se sont estompés), sont également des fonctions sinusoïdales de même fréquence que les sources et dont l'amplitude et la phase à l'origine du temps sont constantes.

Le formalisme des impédances établit quelques règles de calculs des potentiels et des intensités du courant en tout point d'un circuit alimenté par diverses sources et comportant des éléments inductifs et capacitifs. Les méthodes de calcul sont alors similaires à celles utilisées pour les circuits en courant continu. Ce qui montre l'avantage d'employer les impédances.

Ces règles ne sont valables que :

• En régime sinusoïdal établi, c’est-à-dire avec des sources de tension et de courant sinusoïdales et une fois les phénomènes transitoires de départ disparus.
• Avec des composants linéaires, c’est-à-dire des composants dont l'équation caractéristique (relation entre la tension à leurs bornes et l'intensité du courant qui les traverse) est une équation différentielle à coefficients constants. Des composants non linéaires comme les diodes sont exclus. Les bobines à noyau ferromagnétique donneront seulement des résultats approchés et ce, à condition de ne pas dépasser les valeurs d'intensité au-dessus de laquelle leur fonctionnement ne peut plus être considéré comme linéaire suite à la saturation qui intervient dans ces matériaux.

Si toutes les sources n'ont pas la même fréquence ou si les signaux ne sont pas sinusoïdaux, on peut décomposer le calcul en plusieurs étapes à chacune desquelles on pourra utiliser le formalisme d'impédances. Voir plus loin dans cet article.

Définitions

Impédance

Soit un composant électrique ou un circuit alimenté par un courant sinusoïdal . Si la tension à ses bornes est , l'impédance du circuit ou du composant est définie comme un nombre complexe Z, dont le module est égal au rapport et dont l'argument est égal à .

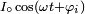
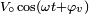
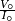
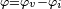
soit

Comme les tensions et les courants sont sinusoïdaux, on peut utiliser aussi bien des valeurs crête (des amplitudes), des valeurs efficaces ou des valeurs crête à crête. Mais il faut faire bien attention à rester uniforme et de ne pas les mélanger. Les résultats des calculs seront du même type que celui utilisé pour les sources.

L'impédance est homogène à une résistance et se mesure en ohms.

Module de l'impédance

Remarque : souvent, par abus de langage on désigne par le terme impédance ce qui, en toute rigueur, devrait s'appeler module de l'impédance.

Le module de l'impédance se mesure en ohms.

Impédance des composants de base

Composants parfaits :

• Résistance : l'impédance d'une résistance R est égale à R :

.

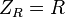
C'est le seul composant à avoir une impédance réelle.

• Bobine : L'impédance d'une bobine d'inductance L est :

.

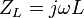
Ici est la pulsation, F la fréquence et j² = -1.

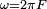
• Condensateur : L'impédance d'un condensateur de capacité C est :

Les composants réels ont des impédances d'expression complexe qui dépend généralement de la fréquence du courant qui les traverse. Ils sont alors modélisés par des circuits constitués de composants idéaux. Par exemple, une résistance réelle présente, en général, une inductance en série avec sa résistance. Une résistance bobinée ressemble à s'y méprendre à une inductance et elle présente une valeur d'inductance significative. En haute fréquence, il est nécessaire d'adjoindre à ce modèle un condensateur en parallèle pour tenir compte des effets capacitifs existants entre deux spires contigües.

De même, un condensateur et une bobine réels peuvent être modélisés en ajoutant une résistance en série ou en parallèle avec la capacité ou l'inductance pour tenir compte des défauts et pertes. Il faut même parfois ajouter des inductances au modèle du condensateur et des capacités au modèle d'inductance. Ces composantes parasites de l'impédance influent significativement sur l'impédance basique au-delà d'une fréquence qui peut varier de quelques kiloHertz à quelques gigaHertz.

Réactance

Une impédance peut être représentée comme la somme d'une partie réelle plus une partie imaginaire :

est la partie résistive et est la partie réactive ou réactance.

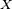
Admittance

Voir article principal admittance. L'admittance est l'inverse de l'impédance :

La conductance est la partie réelle de l'admittance et la susceptance est la partie imaginaire de l'admittance. L'admittance, la conductance et la susceptance se mesurent en siemens. Un siemens est l'inverse d'un ohm.