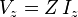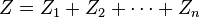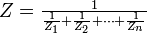Impédance (électricité) - Définition
La liste des auteurs de cet article est disponible ici.
Diagramme de Fresnel
On peut représenter les tensions des sources et les tensions aux bornes des composants d'un circuit comme des vecteurs dans le plan complexe. Avec un peu d'habitude et un minimum de connaissances de géométrie, ces dessins sont beaucoup plus explicites que les valeurs ou des formules. Évidemment ces représentations ne sont pas un moyen de calcul, mais un moyen de « voir » comment les tensions s'additionnent. Ils peuvent être aussi un moyen d'écrire les formules finales en partant des propriétés géométriques. Vous trouverez deux exemples de diagrammes de Fresnel dans les exemples plus bas.
Sources de tension ou de courant déphasées
Si, dans un circuit, on a plusieurs sources de tension ou de courant, on choisit une d'entre elles comme source de référence de phase. Par exemple, si la source prise comme référence est de la forme
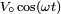
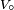

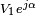
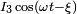
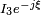
Interprétation des résultats
Le résultat du calcul d'une tension ou d'un courant est, en général, un nombre complexe. Ce nombre complexe s'interprète de la façon suivante :
- Le module indique la valeur de la tension ou du courant calculé. Si les valeurs utilisées pour les sources étaient des valeurs crête, le résultat sera aussi une valeur crête. Si les valeurs utilisées étaient des valeurs efficaces, le résultat sera aussi une valeur efficace.
- L'argument de ce nombre complexe donne le déphasage par rapport à la source utilisée comme référence de phase. Si l'argument est positif, la tension ou le courant calculés seront en avance de phase.
Calcul de circuits avec les impédances
Avec ce qui vient d'être dit, on peut calculer des circuits comprenant des impédances de manière similaire a celle utilisée pour le calcul avec des résistances en courant continu.
Lois de Kirchhoff
Les lois de Kirchhoff s'appliquent de la même manière: « la somme des courants arrivant sur un nœud est nulle » et « la somme des tensions autour d'une maille est nulle ». Cette fois, aussi bien les courants que les tensions sont représentés par des nombres complexes. (Voir transformation complexe).
Généralisation de la loi d'Ohm
La tension aux bornes d'une impédance est égale au produit de l'impédance par le courant :
Aussi bien l'impédance que le courant et la tension sont, en général, complexes.
Impédances en série ou en parallèle
Les impédances en série ou en parallèle se traitent comme les résistances avec la loi d'Ohm. L'impédance de plusieurs impédances en série est égale à leur somme :
L'impédance de plusieurs impédances en parallèle est égale à l'inverse de la somme de leurs inverses :
Quand les impédances ne sont pas directement utilisables
Si toutes les sources n'ont pas la même fréquence, le formalisme des impédances n'est pas directement utilisable. Dans ce cas on peut utiliser le théorème de superposition et faire un calcul séparé pour chacune des fréquences (en remplaçant chaque source de tension de fréquence différente par un court-circuit et chaque source de courant de fréquence différente par un circuit ouvert). Chacune des tensions et courants totales du circuit sera la somme de chacune des tensions ou courants obtenus pour chacune des fréquences. Pour faire ces dernières sommes, il faut exprimer chacune des tensions obtenus avec leur dépendance avec le temps et leur déphasage :
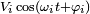
Si les signaux ne sont pas sinusoïdaux mais qu'ils sont périodiques et continus, on peut décomposer les signaux en série de Fourier et utiliser le théorème de superposition et faire un calcul séparé pour chacune des fréquences du développement. Le résultat final sera la somme des résultats obtenus pour chacune des fréquences (avec leur dépendance temporelle et leur déphasage).