Interactions logiques - Définition

Notion d’« interaction logique »

Puisque la variable artificielle « A*B » = -A.B correspond au « ou exclusif » de la logique, il est naturel de s'intéresser aussi à une « interaction logique » beaucoup plus fréquente en physique, à savoir le « et » logique : « A&B ».

Dans le cas des variables à 2 niveaux, la colonne « A&B » aura les valeurs suivantes (valeur forte seulement si A et B sont forts):

	A	B	A.B	A*B	A&B	Y
Essai 1	-1	-1	1	-1	-1	10
Essai 2	-1	1	-1	1	-1	21
Essai 3	1	-1	-1	1	-1	19
Essai 4	1	1	1	-1	1	9

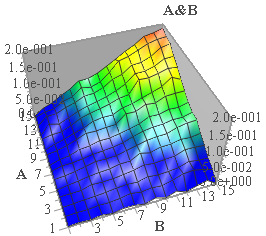
Et, dans le cas général des variables continues, nous avons la figure suivante :

Figure 5 : surface de réponse du « Et logique »

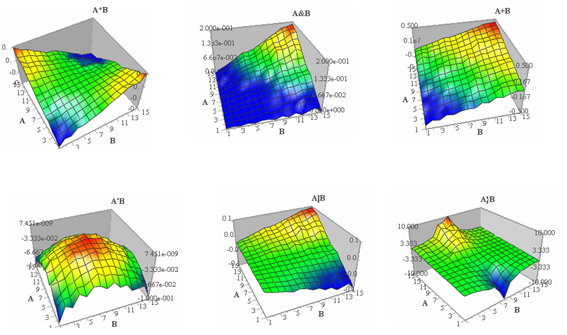
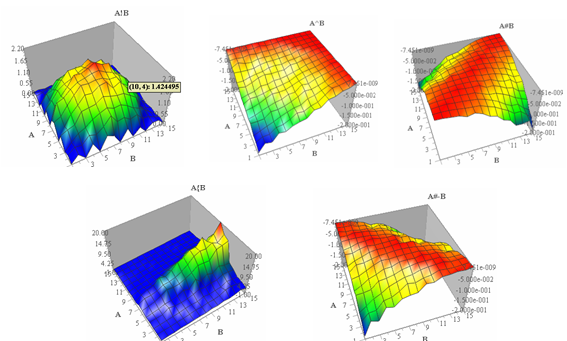
Les figures suivantes montrent d’autres "interactions logiques", dont on trouvera la description ci-après, et les formules mathématiques en références.

Interprétation physique du produit croisé

L’interprétation physique du produit de deux variables de même unité, comme la longueur et la largeur, est aisée (c’est une surface).

Mais que signifie l’effet sur Y du produit croisé A.B de deux variables qui étaient à l'origine d’unités différentes, et qui ont été centrées réduites ?

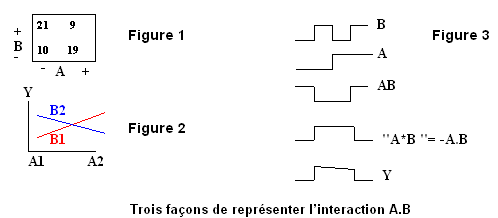
Figure 1 : A en abscisse, B en ordonnée ; et les valeurs correspondantes de Y. La variable à expliquer Y est faible si A et B sont faibles, ou bien si A et B sont forts.

Figure 2 :

• en rouge : variation de Y en fonction de A, pour B faible ;

• en bleu : variation de Y en fonction de A, pour B fort.

Y varie donc de façon différente en fonction de A, selon que B est faible ou fort.

Figure 3 : profils de variation, en fonction de la suite des essais : Y ressemble surtout à « A*B ». Ou si l’on préfère, Y est corrélé positivement avec « A*B » et négativement avec A.B.

Ces figures montrent que Y est fort si A est faible et B est fort, ou bien si A est fort et B est faible.

En d’autres termes l’opération « A*B » = -A.B correspond au « ou exclusif » de la logique.

La figure 1 représentait le « ou exclusif » dans le cas où les variables A et B sont discontinues à deux niveaux.

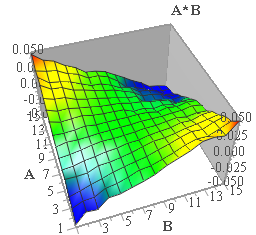
Dans le cas où les variables A et B sont continues, on obtient la figure 4 caractérisée par des « montagnes » en rouge lorsque A est fort et B faible, ou bien A est faible et B est fort. Dans le cas contraire, il y a des « vallées » (en bleu).

Figure 4 : surfaces de réponse de la variable A*B

Signification des symboles d’interactions logiques

f(A,B)	Signification	La réponse Y est forte lorsque...
A*B	A ou-exclusif B	...A est fort et B faible ou A est faible et B fort
A^B	A ou B	...A est fort ou B est fort
A^-B	A ou non B	...A est fort ou B est faible
A&B	A et B	...A et B sont forts
A&-B	A et non B	...A est fort et B est faible
A]B	A modulé par B	...A est fort si B est fort
A]-B	A modulé par non B	...A est fort si B est faible
A}B	A modulé par B moyen	...A est fort si B est moyen
A{B	A moyen si B	...A est moyen si B est fort
A{-B	A moyen si non B	...A est moyen si B est faible
A'B	ni A ni B (sens large)	...ni A ni B ne sont extrêmes (ils sont moyens)
A!B	ni A ni B (sens strict)	...ni A ni B ne sont extrêmes (ils sont strictement moyens)
A#B	A comme B	...A varie comme B
A+B	"A plus B"	...la somme de A et B (centrés-réduits) est forte
A-B	"A moins B"	...la différence de A et B (centrés-réduits) est forte