Intersection (mathématiques) - Définition

Introduction

Intersection des ensembles A et B

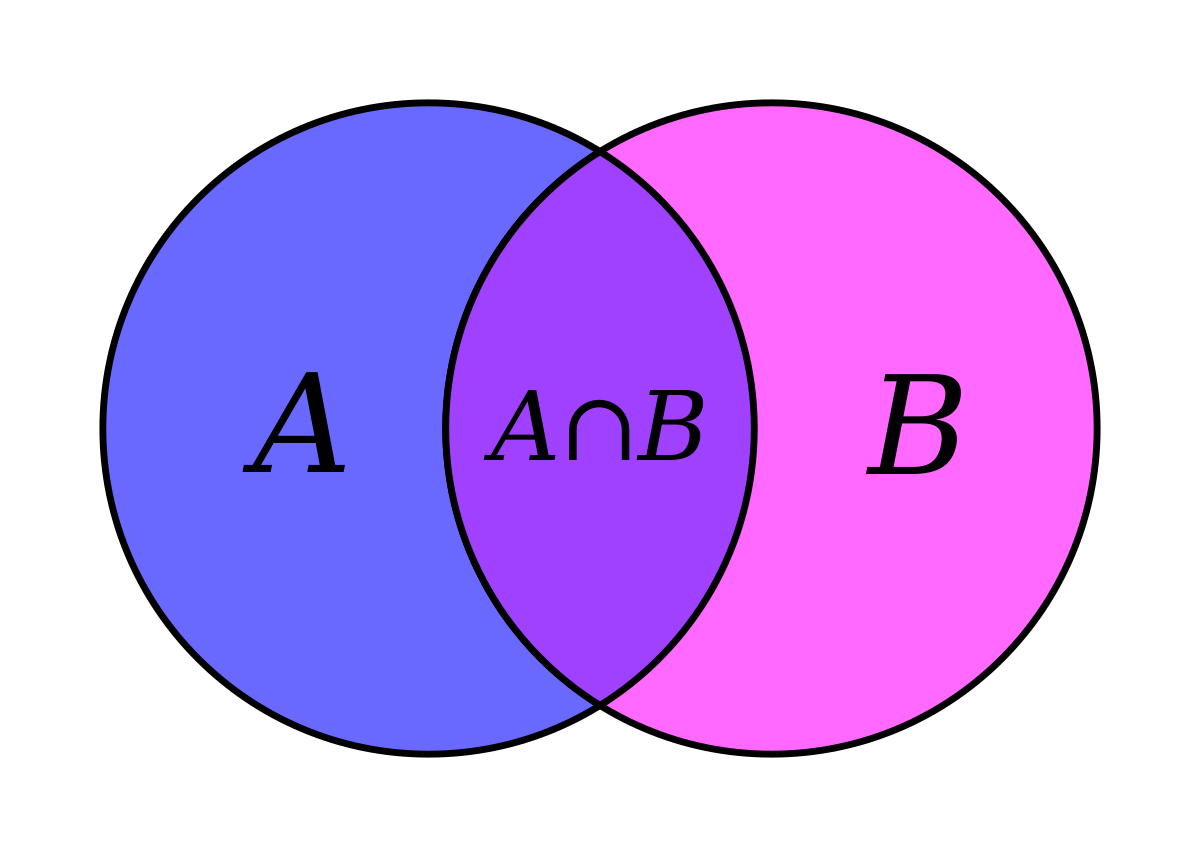
Dans la théorie des ensembles, l'intersection de deux ensembles A et B est l'ensemble qui contient tous les éléments qui appartiennent à la fois à A et à B, et seulement ceux-là.

L'intersection de A et B est notée A∩B.

L'intersection de deux ensembles quelconques existe toujours. Si les ensembles A et B n'ont aucun élément en commun, on dit que leur intersection est vide ; on écrit : A ∩ B = .

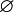
Si tous les éléments de A sont éléments de B (si A est inclus dans B), alors A ∩ B = A .

Exemples en géométrie

Intersection de deux droites

Dans le plan

• Dans le plan, l'intersection de deux droites ni parallèles ni confondues est un point : . On dit qu'elles sont sécantes.
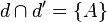
• Si deux droites sont parallèles mais distinctes, elles n'ont pas de point commun ; leur intersection est vide :
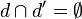
• Si deux droites sont confondues, tous leurs points sont communs, l'intersection est une droite.

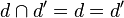
Dans l'espace

• Dans l'espace, deux droites sont non-coplanaires n'ont aucun point commun ; leur intersection est vide : .
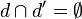
• Deux droites parallèles ou sécantes sont coplanaires.

Autres exemples

Dans l'espace

• l'intersection de une droite et un plan non parallèles est un point
• l'intersection de deux plans non parallèles est une droite.

Dans le plan

• l'intersection d'une droite et d'un cercle est formée de zéro, un ou deux points, selon que la distance du centre du cercle à la droite est supérieure, égale ou inférieure au rayon du cercle. Si l'intersection est réduite à un point, la droite est tangente au cercle.
• l'intersection de deux cercles est formée de deux points si la distance entre leurs centres est (strictement) inférieure à la somme de leurs rayons et supérieure à leur différence, d'un point si cette distance est égale à la somme ou à la différence des rayons (cercles tangents), vide dans les autres cas.

En algèbre booléenne

En algèbre booléenne, l'intersection est associée à l'opérateur logique et : si A est l'ensemble des éléments de E possédant la propriété P (ou satisfaisant la condition P ) et B l'ensemble des éléments de E possédant la propriété Q (ou satisfaisant la condition Q ), alors A ∩ B est l'ensemble des éléments de E possédant la propriété PetQ (ou satisfaisant à la fois la condition P et la condition Q ).

Exemple 1: si E est l'ensemble des entiers naturels inférieurs à 10, A l'ensemble des éléments de E impairs, et B l'ensemble des éléments de E premiers, alors A ∩ B est l'ensemble des éléments de E impairs et premiers :

A = {1, 3, 5, 7, 9} , B = {2, 3, 5, 7} , A ∩ B = {3, 5, 7}

Exemple 2: l'intersection de l'ensemble des rectangles (quadrilatères ayant leurs quatre angles droits) et de l'ensemble des losanges (quadrilatères ayant leurs quatre côtés égaux) est l'ensemble des carrés (quadrilatères ayant leurs quatre angles droits et leurs quatre côtés égaux).

En géométrie analytique

En géométrie analytique, l'intersection de deux objets est défini par le système d'équations formé par la réunion des équations associées à chaque objet.

En dimension 2, l'intersection de deux droites est définie par un système de deux équations à 2 inconnues, qui a, en général, une solution unique, sauf si son déterminant est nul, auquel cas il en a soit zéro soit une infinité : on retrouve les trois cas de la géométrie.

En dimension 3, l'intersection de trois plans est définie par un système de trois équations à 3 inconnues, qui a, en général, une solution unique, sauf si son déterminant est nul.