Liste des polyèdres uniformes - Définition

Introduction

Les polyèdres uniformes et les pavages forment un groupe bien étudié. Ils sont listés ici pour une comparaison rapide de leurs propriétés et de leurs noms de schéma variés ainsi que de leurs symboles.

Cette liste inclut :

• tous les 75 polyèdres uniforme non-prismatiques;
• tous les 11 pavages uniformes avec des faces convexes;
• quelques représentation des ensembles infinis des prismes et des antiprismes;
• un polyèdre particulier, le polyèdre de Skilling avec des arêtes qui se chevauchent.

Ce qui n'est pas inclus :

• 40 polyèdres uniformes potentiels avec des figures de sommet dégénérées qui ont des arêtes qui se chevauchent (non comptés par Coxeter);
• 14 pavages uniformes avec des faces non-convexes;
• l'ensemble infini des pavages hyperboliques uniformes.

Table des polyèdres

Les formes convexes sont listées en ordre de degrés de configuration de sommet à partir de 3 faces/sommet et au-dessus, et en augmentant les côtés par face. Cet ordre permet de montrer des similarités topologiques.

Formes convexes (3 faces/sommet)

Nom	Image	Classe de solide	Symbole de Wythoff	Figure de sommet	Acronyme de Bowers	Groupe de symétrie	W#	U#	K#	Sommets	Arêtes	Faces	Chi	Faces par type
Tétraèdre		R	3|2 3	3.3.3	Tet	Td	W001	U01	K06	4	6	4	2	4{3}
Prisme triangulaire		P	2 3|2	3.4.4	Trip	D3h	--	--	--	6	9	5	2	2{3}+3{4}
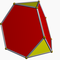
Tétraèdre tronqué		A	2 3|3	3.6.6	Tut	Td	W006	U02	K07	12	18	8	2	4{3}+4{6}
Cube tronqué		A	2 3|4	3.8.8	Tic	Oh	W008	U09	K14	24	36	14	2	8{3}+6{8}
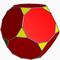
Dodécaèdre tronqué		A	2 3|5	3.10.10	Tid	Ih	W010	U26	K31	60	90	32	2	20{3}+12{10}
Pavage hexagonal tronqué		T	2 3|6	3.12.12	Toxat	P6m	--	--	--	6n	9n	3n	0	n{12}+2n{3}
Pavage heptagonal tronqué		T	2 3|7	3.14.14	--	*732	--	--	--				0
Cube		R	3|2 4	4.4.4	Cube	Oh	W003	U06	K11	8	12	6	2	6{4}
Prisme pentagonal		P	2 5|2	4.4.5	Pip	D5h	--	U76	K01	10	15	7	2	5{4}+2{5}
Prisme hexagonal		P	2 6|2	4.4.6	Hip	D6h	--	--	--	12	18	8	2	6{4}+2{6}
Prisme octogonal		P	2 8|2	4.4.8	Op	D8h	--	--	--	16	24	10	2	8{4}+2{8}
Prisme décagonal		P	2 10|2	4.4.10	Dip	D10h	--	--	--	20	30	12	2	10{4}+2{10}
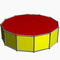
Prisme dodécagonal		P	2 12|2	4.4.12	Twip	D12h	--	--	--	24	36	14	2	12{4}+2{12}
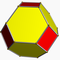
Octaèdre tronqué		A	2 4|3	4.6.6	Toe	Oh	W007	U08	K13	24	36	14	2	6{4}+8{6}
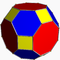
Grand rhombicuboctaèdre		A	2 3 4|	4.6.8	Girco	Oh	W015	U11	K16	48	72	26	2	12{4}+8{6}+6{8}
Grand rhombicosidodécaèdre		A	2 3 5|	4.6.10	Grid	Ih	W016	U28	K33	120	180	62	2	30{4}+20{6}+12{10}
Pavage grand rhombitrihexagonal		T	2 3 6|	4.6.12	Othat	p6m	--	--	--	12n	18n	6n	0	3n{4}+2n{6}+n{12}
Pavage grand rhombitriheptagonal		T	2 3 7|	4.6.14	--	*732	--	--	--	14n	21n	7n	0	3n{4}+2n{7}+n{14}
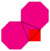
Pavage carré tronqué		T	2 4|4	4.8.8	Tosquat	p4m	--	--	--	4n	6n	2n	0	n{4}+n{8}
Dodécaèdre		R	3|2 5	5.5.5	Doe	Ih	W005	U23	K28	20	30	12	2	12{5}
Icosaèdre tronqué		A	2 5|3	5.6.6	Ti	Ih	W009	U25	K30	60	90	32	2	12{5}+20{6}
Pavage triangulaire tronqué d'ordre 7		T	2 7|3	7.6.6	--	*732	--	--	--				0
Pavage hexagonal		T	3|2 6	6.6.6	Hexat	p6m	--	--	--	2n	3n	n	0	n{6}
Pavage heptagonal d'ordre 3		T	3|2 7	7.7.7	-	*732	--	--	--	2n	3n	n	0	n{7}

Formes convexes (4 faces/sommet)

Nom	Image	Classe de solide	Symbole de Wythoff	Figure de sommet	Acronyme de Bowers	Groupe de symétrie	W#	U#	K#	Sommets	Arêtes	Faces	Chi	Faces par type
Octaèdre		R	4|2 3	3.3.3.3	Oct	Oh	W002	U05	K10	6	12	8	2	8{3}
Antiprisme carré		P	|2 2 4	3.3.3.4	Squap	D4d	--	--	--	8	16	10	2	8{3}+2{4}
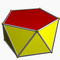
Antiprisme pentagonal		P	|2 2 5	3.3.3.5	Pap	D5d	--	U77	K02	10	20	12	2	10{3}+2{5}
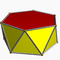
Antiprisme hexagonal		P	|2 2 6	3.3.3.6	Hap	D6d	--	--	--	12	24	14	2	12{3}+2{6}
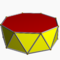
Antiprisme octogonal		P	|2 2 8	3.3.3.8	Oap	D8d	--	--	--	16	32	18	2	16{3}+2{8}
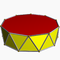
Antiprisme décagonal		P	|2 2 10	3.3.3.10	Dap	D10d	--	--	--	20	40	22	2	20{3}+2{10}
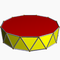
Antiprisme dodécagonal		P	|2 2 12	3.3.3.12	Twap	D12d	--	--	--	24	48	26	2	24{3}+2{12}
Cuboctaèdre		A	2|3 4	3.4.3.4	Co	Oh	W011	U07	K12	12	24	14	2	8{3}+6{4}
Petit rhombicuboctaèdre		A	3 4|2	3.4.4.4	Sirco	Oh	W013	U10	K15	24	48	26	2	8{3}+(6+12){4}
Petit rhombicosidodécaèdre		A	3 5|2	3.4.5.4	Srid	Ih	W014	U27	K32	60	120	62	2	20{3}+30{4}+12{5}
Petit pavage rhombitrihexagonal		T	3 6|2	3.4.6.4	Rothat	p6m	--	--	--	6n	12n	6n	0	2n{3}+3n{4}+n{6}
Icosidodécaèdre		A	2|3 5	3.5.3.5	Id	Ih	W012	U24	K29	30	60	32	2	20{3}+12{5}
Pavage trihexagonal		T	2|3 6	3.6.3.6	That	p6m	--	--	--	3n	6n	3n	0	2n{3}+n{6}
Pavage triheptagonal		T	2|3 6	3.7.3.7	--	*732	--	--	--	3n	6n	3n	0	2n{3}+n{7}
Pavage carré		T	4|2 4	4.4.4.4	Squat	p4m	--	--	--	n	2n	n	0	n{4}

Formes convexes (5 faces/sommet)

Nom	Image	Classe de solide	Symbole de Wythoff	Figure de sommet	Acronyme de Bowers	Groupe de symétrie	W#	U#	K#	Sommets	Arêtes	Faces	Chi	Faces par type
Icosaèdre		R	5|2 3	3.3.3.3.3	Ike	Ih	W004	U22	K27	12	30	20	2	20{3}
Cube adouci		A	|2 3 4	3.3.3.3.4	Snic	O	W017	U12	K17	24	60	38	2	(8+24){3}+6{4}
Dodécaèdre adouci		A	|2 3 5	3.3.3.3.5	Snid	I	W018	U29	K34	60	150	92	2	(20+60){3}+12{5}
Pavage hexagonal adouci		T	|2 3 6	3.3.3.3.6	Snathat	p6	--	--	--	6n	15n	9n	0	8n{3}+n{6}
Pavage triangulaire allongé		T	|2 2 (2|2)	3.3.3.4.4	Etrat	cmm	--	--	--	2n	5n	3n	0	2n{3}+n{4}
Pavage carré adouci		T	|2 4 4	3.3.4.3.4	Snasquat	p4g	--	--	--	4n	10n	6n	0	4n{3}+2n{4}

Formes convexes (6 faces/sommet)

Nom	Image	Classe de solide	Symbole de Wythoff	Figure de sommet	Acronyme de Bowers	Groupe de symétrie	W#	U#	K#	Sommets	Arêtes	Faces	Chi	Faces par type
Pavage triangulaire		T	6|2 3	3.3.3.3.3.3	Trat	p6m	--	--	--	n	3n	2n	0	2n{3}

Formes convexes (7 faces/sommet)

Nom	Image	Classe de solide	Symbole de Wythoff	Figure de sommet	Acronyme de Bowers	Groupe de symétrie	W#	U#	K#	Sommets	Arêtes	Faces	Chi	Faces par type
Pavage triangulaire d'ordre 7		T	7|2 3	3.3.3.3.3.3.3	--	*732	--	--	--	n	3n	2n	0	2n{3}

Formes non-convexes avec des faces convexes

Nom	Image	Classe de solide	Symbole de Wythoff	Figure de sommet	Acronyme de Bowers	Groupe de symétrie	W#	U#	K#	Sommets	Arêtes	Faces	Chi	Faces par type
Tétrahémihexaèdre		C+	3/2 3|2	4.3/2.4.3	Thah	Td	W067	U04	K09	6	12	7	1	4{3}+3{4}
Cubohémioctaèdre		C+	4/3 4|3	6.4/3.6.4	Cho	Oh	W078	U15	K20	12	24	10	-2	6{4}+4{6}
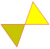
Octahémioctaèdre		C+	3/2 3|3	6.3/2.6.3	Oho	Oh	W068	U03	K08	12	24	12	0	8{3}+4{6}
Grand dodécaèdre		R+	5/2|2 5	(5.5.5.5.5)/2	Gad	Ih	W021	U35	K40	12	30	12	-6	12{5}
Grand icosaèdre		R+	5/2|2 3	(3.3.3.3.3)/2	Gike	Ih	W041	U53	K58	12	30	20	2	20{3}
Grand icosidodécaèdre ditrigonal		C+	3/2|3 5	(5.3.5.3.5.3)/2	Gidtid	Ih	W087	U47	K52	20	60	32	-8	20{3}+12{5}
Petit rhombihexaèdre		C+	3/2 2 4|	4.8.4/3.8	Sroh	Oh	W086	U18	K23	24	48	18	-6	12{4}+6{8}
Petit cubicuboctaèdre		C+	3/2 4|4	8.3/2.8.4	Socco	Oh	W069	U13	K18	24	48	20	-4	8{3}+6{4}+6{8}
Grand rhombicuboctaèdre uniforme		C+	3/2 4|2	4.3/2.4.4	Querco	Oh	W085	U17	K22	24	48	26	2	8{3}+(6+12){4}
Petit dodécahémidodécaèdre		C+	5/4 5|5	10.5/4.10.5	Sidhid	Ih	W091	U51	K56	30	60	18	-12	12{5}+6{10}
Petit icosihémidodécaèdre		C+	3/2 3|5	10.3/2.10.3	Seihid	Ih	W089	U49	K54	30	60	26	-4	20{3}+6{10}
Petit dodécicosaèdre		C+	3/2 3 5|	10.6.10/9.6/5	Siddy	Ih	W090	U50	K55	60	120	32	-28	20{6}+12{10}
Petit rhombidodécaèdre		C+	2 5/2 5|	10.4.10/9.4/3	Sird	Ih	W074	U39	K44	60	120	42	-18	30{4}+12{10}
Petit dodécicosidodécaèdre		C+	3/2 5|5	10.3/2.10.5	Saddid	Ih	W072	U33	K38	60	120	44	-16	20{3}+12{5}+12{10}
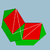
Rhombicosaèdre		C+	2 5/2 3|	6.4.6/5.4/3	Ri	Ih	W096	U56	K61	60	120	50	-10	30{4}+20{6}
Grand icosicosidodécaèdre		C+	3/2 5|3	6.3/2.6.5	Giid	Ih	W088	U48	K53	60	120	52	-8	20{3}+12{5}+20{6}

Formes prismatiques non-convexes

Nom	Image	Classe de solide	Symbole de Wythoff	Figure de sommet	Acronyme de Bowers	Groupe de symétrie	W#	U#	K#	Sommets	Arêtes	Faces	Chi	Faces par type
Prisme pentagrammique		P+	2 5/2|2	5/2.4.4	Stip	D5h	--	U78	K03	10	15	7	2	5{4}+2{5/2}
Prisme heptagrammique (7/3)		P+	2 7/3|2	7/3.4.4	Giship	D7h	--	--	--	14	21	9	2	7{4}+2{7/3}
Prisme heptagrammique (7/2)		P+	2 7/2|2	7/2.4.4	Ship	D7h	--	--	--	14	21	9	2	7{4}+2{7/2}
Antiprisme pentagrammique		P+	|2 2 5/2	5/2.3.3.3	Stap	D5h	--	U79	K04	10	20	12	2	10{3}+2{5/2}
Antiprisme pentagrammique croisé		P+	|2 2 5/3	5/3.3.3.3	Starp	D5d	--	U80	K05	10	20	12	2	10{3}+2{5/2}

Autres formes non-convexes avec des faces non-convexes

Nom	Image	Classe de solide	Symbole de Wythoff	Figure de sommet	Acronyme de Bowers	Groupe de symétrie	W#	U#	K#	Sommets	Arêtes	Faces	Chi	Faces par type
Petit dodécaèdre étoilé		R+	5|2 5/2	(5/2)5	Sissid	Ih	W020	U34	K39	12	30	12	-6	12{5/2}
Grand dodécaèdre étoilé		R+	3|2 5/2	(5/2)3	Gissid	Ih	W022	U52	K57	20	30	12	2	12{5/2}
Dodécadodécaèdre ditrigonal		S+	3|5/3 5	(5/3.5)3	Ditdid	Ih	W080	U41	K46	20	60	24	-16	12{5}+12{5/2}
Petit icosidodécaèdre ditrigonal		S+	3|5/2 3	(5/2.3)3	Sidtid	Ih	W070	U30	K35	20	60	32	-8	20{3}+12{5/2}
Hexaèdre tronqué étoilé		S+	2 3|4/3	8/3.8/3.3	Quith	Oh	W092	U19	K24	24	36	14	2	8{3}+6{8/3}
Grand rhombihexaèdre		S+	4/33/2 2|	4.8/3.4/3.8/5	Groh	Oh	W103	U21	K26	24	48	18	-6	12{4}+6{8/3}
Grand cubicuboctaèdre		S+	3 4|4/3	8/3.3.8/3.4	Gocco	Oh	W077	U14	K19	24	48	20	-4	8{3}+6{4}+6{8/3}
Grand dodécahémidodécaèdre		S+	5/35/2|5/3	10/3.5/3.10/3.5/2	Gidhid	Ih	W107	U70	K75	30	60	18	-12	12{5/2}+6{10/3}
Petit dodécahémicosaèdre		S+	5/35/2|3	6.5/3.6.5/2	Sidhei	Ih	W100	U62	K67	30	60	22	-8	12{5/2}+10{6}
Grand dodécahémicosaèdre		S+	5/4 5|3	6.5/4.6.5	Gidhei	Ih	W102	U65	K70	30	60	22	-8	12{5}+10{6}
Dodécadodécaèdre		S+	2|5/2 5	(5/2.5)2	Did	Ih	W073	U36	K41	30	60	24	-6	12{5}+12{5/2}
Grand icosihémidodécaèdre		S+	3/2 3|5/3	10/3.3/2.10/3.3	Geihid	Ih	W106	U71	K76	30	60	26	-4	20{3}+6{10/3}
Grand icosidodécaèdre		S+	2|5/2 3	(5/2.3)2	Gid	Ih	W094	U54	K59	30	60	32	2	20{3}+12{5/2}
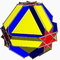
Cuboctaèdre cubitronqué		S+	4/3 3 4|	8/3.6.8	Cotco	Oh	W079	U16	K21	48	72	20	-4	8{6}+6{8}+6{8/3}
Grand cuboctaèdre tronqué		S+	4/3 2 3|	8/3.4.6	Quitco	Oh	W093	U20	K25	48	72	26	2	12{4}+8{6}+6{8/3}
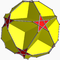
Grand dodécaèdre tronqué		S+	2 5/2|5	10.10.5/2	Tigid	Ih	W075	U37	K42	60	90	24	-6	12{5/2}+12{10}
Petit dodécaèdre étoilé tronqué		S+	2 5|5/3	10/3.10/3.5	Quitsissid	Ih	W097	U58	K63	60	90	24	-6	12{5}+12{10/3}
Grand dodécaèdre étoilé tronqué		S+	2 3|5/3	10/3.10/3.3	Quitgissid	Ih	W104	U66	K71	60	90	32	2	20{3}+12{10/3}
Grand icosaèdre tronqué		S+	2 5/2|3	6.6.5/2	Tiggy	Ih	W095	U55	K60	60	90	32	2	12{5/2}+20{6}
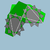
Grand dodécicosaèdre		S+	5/35/2 3|	6.10/3.6/5.10/7	Giddy	Ih	W101	U63	K68	60	120	32	-28	20{6}+12{10/3}
Grand rhombidodécaèdre		S+	3/25/3 2|	4.10/3.4/3.10/7	Gird	Ih	W109	U73	K78	60	120	42	-18	30{4}+12{10/3}
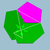
Icosidodécadodécaèdre		S+	5/3 5|3	6.5/3.6.5	Ided	Ih	W083	U44	K49	60	120	44	-16	12{5}+12{5/2}+20{6}
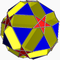
Petit dodécicosidodécaèdre ditrigonal		S+	5/3 3|5	10.5/3.10.3	Sidditdid	Ih	W082	U43	K48	60	120	44	-16	20{3}+12{;5/2}+12{10}
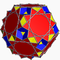
Grand dodécicosidodécaèdre ditrigonal		S+	3 5|5/3	10/3.3.10/3.5	Gidditdid	Ih	W081	U42	K47	60	120	44	-16	20{3}+12{5}+12{10/3}
Grand dodécicosidodécaèdre		S+	5/2 3|5/3	10/3.5/2.10/3.3	Gaddid	Ih	W099	U61	K66	60	120	44	-16	20{3}+12{5/2}+12{10/3}
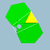
Petit icosicosidodécaèdre		S+	5/2 3|3	6.5/2.6.3	Siid	Ih	W071	U31	K36	60	120	52	-8	20{3}+12{5/2}+20{6}
Rhombidodécadodécaèdre		S+	5/2 5|2	4.5/2.4.5	Raded	Ih	W076	U38	K43	60	120	54	-6	30{4}+12{5}+12{5/2}
Grand rhombicosidodécaèdre uniforme		S+	5/3 3|2	4.5/3.4.3	Qrid	Ih	W105	U67	K72	60	120	62	2	20{3}+30{4}+12{5/2}
Dodécadodécaèdre adouci		S+	|2 5/2 5	3.3.5/2.3.5	Siddid	I	W111	U40	K45	60	150	84	-6	60{3}+12{5}+12{5/2}
Dodécadodécaèdre adouci inversé		S+	|5/3 2 5	3.5/3.3.3.5	Isdid	I	W114	U60	K65	60	150	84	-6	60{3}+12{5}+12{5/2}
Grand icosidodécaèdre adouci		S+	|2 5/2 3	3.4.5/2	Gosid	I	W116	U57	K62	60	150	92	2	(20+60){3}+12{5/2}
Grand icosidodécaèdre adouci inversé		S+	|5/3 2 3	3.3.5/3	Gisid	I	W113	U69	K74	60	150	92	2	(20+60){3}+12{5/2}
Grand icosidodécaèdre rétroadouci		S+	|3/25/3 2	(34.5/2)/2	Girsid	I	W117	U74	K79	60	150	92	2	(20+60){3}+12{5/2}
Grand dodécicosidodécaèdre adouci		S+	|5/35/2 3	33.5/3.3.5/2	Gisdid	I	W115	U64	K69	60	180	104	-16	(20+60){3}+(12+12){5/2}
Icosidodécadodécaèdre adouci		S+	|5/3 3 5	3.3.5.5/3	Sided	I	W112	U46	K51	60	180	104	-16	(20+60){3}+12{5}+12{5/2}
Petit icosicosidodécaèdre adouci		S+	|5/2 3 3	35.5/2	Seside	Ih	W110	U32	K37	60	180	112	-8	(40+60){3}+12{5/2}
Petit icosicosidodécaèdre rétroadouci		S+	|3/23/25/2	(35.5/3)/2	Sirsid	Ih	W118	U72	K77	60	180	112	-8	(40+60){3}+12{5/2}
Grand dirhombicosidodécaèdre		S+	|3/25/3 3 5/2		Gidrid	Ih	W119	U75	K80	60	240	124	-56	40{3}+60{4}+24{5/2}
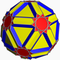
Dodécadodécaèdre icositronqué		S+	5/3 3 5|	10/3.6.10	Idtid	Ih	W084	U45	K50	120	180	44	-16	20{6}+12{10}+12{10/3}
Dodécadodécaèdre tronqué		S+	5/3 2 5|	10/3.4.10	Quitdid	Ih	W098	U59	K64	120	180	54	-6	30{4}+12{10}+12{10/3}
Grand icosidodécaèdre tronqué		S+	5/3 2 3|	10/3.4.6	Gaquatid	Ih	W108	U68	K73	120	180	62	2	30{4}+20{6}+12{10/3}

Cas particulier

Nom	Image	Classe de solide	Symbole de Wythoff	Figure de sommet	Acronyme de Bowers	Groupe de symétrie	W#	U#	K#	Sommets	Arêtes	Faces	Chi	Faces par type
Grand dirhombidodécaèdre disadouci Polyèdre de Skilling		S++	| (3/2) 5/3 (3) 5/2		--	Ih	--	--	--	60	240 (*1)	204	24	120{3}+60{4}+24{5/2}

(*1) : Le grand dirhombidodécaèdre disadouci possède 120 arêtes partagées par quatre faces. Si elles sont comptées comme deux paires, alors il existe au total 360 arêtes. À cause de cette dégénérescence des arêtes, il n'est pas toujours considéré comme un polyèdre uniforme.