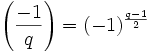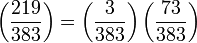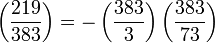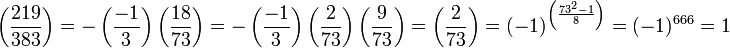Loi de réciprocité quadratique - Définition

Exemples

Avec des nombres premiers

Par exemple, si p vaut 11 et q vaut 19, il est possible de ramener le calcul de à celui de , qui est égal à (puisque ). Pour aller plus loin, nous avons besoin de propriétés supplémentaires qui permettent de calculer et explicitement, par exemple :

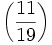
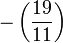
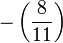
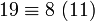
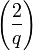
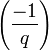
En utilisant cela, nous ramenons successivement le calcul de à (car ), puis à et enfin à , ce qui termine le calcul, puisque 2 n'est pas résidu quadratique modulo 3. . Conclusion : Le résultat étant 1, on en déduit que 11 est résidu quadratique modulo 19. D'ailleurs, on le vérifie immédiatement :

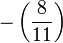
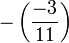
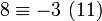
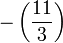
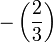
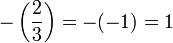
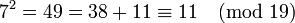
Cas général

Déterminons si 219 est un carré modulo 383. Les propriétés du symbole de Legendre montrent que :

Une première application de la loi de réciprocité quadratique montre que :

En appliquant encore la loi de réciprocité quadratique et les propriétés du symbole de Legendre, on obtient :

Outil de démonstration

Si p est un nombre premier, 5 est-il un carré modulo p ? La loi de réciprocité quadratique nous permet d'affirmer que cela arrive lorsque p est lui-même un carré modulo 5, c'est-à-dire quand

Généralisations

Il existe des lois de réciprocité cubique, biquadratique (c'est-à-dire de degré 4) et ainsi de suite. Cependant la véritable généralisation de toutes ces lois, généralisation monumentale, est la théorie des corps de classes.

Le lemme de Gauss concerne les propriétés des résidus quadratiques et sert dans la démonstration établie par Gauss de la loi de réciprocité quadratique.