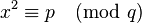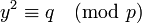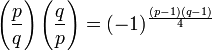Loi de réciprocité quadratique - Définition

Soit p un nombre premier différent de 2. L'objectif est de déterminer le statut quadratique de -1 et 2 dans le corps fini Z/pZ ou encore F_p. La notation F_p désigne l'unique corps fini contenant p éléments, à un isomorphisme près. Ici, F_p^* désigne le groupe multiplicatif du corps F_p. C'est un groupe cyclique contenant p - 1 éléments (cf l'article Anneau Z/nZ). Comme p est premier différent de deux, l'ordre du groupe multiplicatif est toujours pair.

• Structure de l'ensemble Q des résidus quadratiques de F_p^* :

Soit φ l'endomorphisme de groupe de F_p^* qui à x associe x². Son noyau est composé des deux éléments 1 et -1. L'image d'un morphisme de groupe est toujours un sous-groupe. Cette image, par définition égal à l'ensemble des résidus quadratiques Q, est donc un sous-groupe. Le théorème de Lagrange montre que l'ordre de Q est égal à (p - 1 )/2, car 2 est l'ordre du noyau.

Soit ψ le morphisme canonique de F_p^* dans F_p^*/Q. C'est un morphisme dans un groupe à deux éléments dont le noyau est l'ensemble des résidus quadratique, ainsi a est un résidu quadratique si et seulement si ψ(a) = 1. Cette propriété montre que le produit a.b de deux éléments de F_p^* est quadratique si a et b sont simultanément quadratiques ou si aucun des deux ne l'est.

Soit A l'ensemble des résidus quadratiques de F_p^* différents de - 1 et B celui des résidus non quadratiques différents de - 1. On remarque que si b est un élément de B, alors b^-1 est différent de b. En effet, les seuls éléments égaux à leurs inverses sont 1 et -1 et aucun élément de B n'est égal à l'un de ceux là. Le produit de b par b^-1 est égal à 1 donc à un résidu quadratique, ce qui montre que b^-1 n'est pas quadratique car b ne l'est pas non plus. En regroupant dans B les éléments avec leurs inverses, on remarque que l'ordre de B est nécessairement pair.

• Caractère quadratique de -1 dans F_p^* :

Comme p est impair, il est congru soit à 1, soit à 3 modulo 4. Supposons qu'il existe n tel que p - 1 = 4.n. Il existe exactement 2.n résidus quadratiques et donc aussi 2.n résidus non quadratiques. De plus, B est de cardinal pair tout comme l'ensemble des résidus non quadratiques. L'élément -1 est donc nécessairement quadratique.

Supposons qu'il existe n tel que p - 1 = 4.n + 2. Alors il existe exactement 2.n + 1 résidus non quadratiques. B est de cardinal pair, donc -1 est un résidu non quadratique, ce qui termine la démonstration.

Étudions à présent le polynôme formel P(X) de F_p[X] défini par :

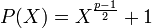
• Racines du polynôme P(X) :

Il admet au plus (p - 1)/2 racines. Le petit théorème de Fermat montre que tout résidu quadratique à la puissance (p - 1)/2 est égal à 1 et tout résidu non quadratique à la même puissance donne une valeur dont le carré est égal à 1 et qui est différent de 1. En conséquence tout résidu non quadratique à la puissance (p - 1)/2 est égal à -1. Et tout résidu non quadratique est racine de P(X). Comme le cardinal de F_p^* - Q est exactement (p - 1)/2, on obtient l'égalité suivante :

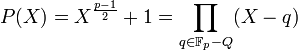
Analysons p en fonction de son reste modulo 8. Soit n et r les deux entiers tel que p = 8.n + r, avec r élément de {1, 3, 5, 7}.

• Caractère quadratique de 2 si r est égal à 1 ou 5 :

Si r est égal à 1 ou 5, alors p - 1 est un multiple de 4. En conséquence, -1 est un résidu quadratique et B est l'ensemble des non résidus quadratiques. Soit C l'ensemble égal à B - 1, c'est à dire l'ensemble des éléments de B auxquels on retranche 1. L'égalité suivante montre que la moitié des élément de C sont des résidus quadratiques et l'autre non :

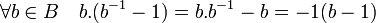
En effet, si b - 1 est un résidu quadratique, comme b ne l'est pas et que -1 l'est, b^-1 - 1 ne l'est pas non plus. Ce qui montre que l'on peut partitionner C en un ensemble de paires dont un élément est un résidu quadratique et l'autre non. Comme (p - 1)/2 est pair, le calcul de P(1) montre que :

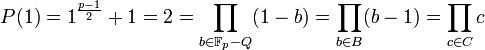
Si r est égal à 1, le cardinal de C, égal à celui de B est égal à 4.n et C contient exactement 2.n résidus non quadratiques. Le produit de tous les éléments de C est donc quadratique, ce qui permet de conclure au caractère quadratique de 2. Si r est égal à 5, le cardinal de C est 4.n + 2 et C contient exactement 2n + 1 résidus non quadratiques. Le produit de tous les éléments de C est non quadratique, ce qui permet de conclure au caractère non quadratique de 2.

• Caractère quadratique de 2 si r est égal à 3 ou 7 :

Pour ces cas, -1 n'est pas dans B et n'est pas un résidu quadratique. Considérons alors l'ensemble C' égal à B + 1. L'égalité suivante et le raisonnement précédent montrent que la moitié des éléments de C' sont des résidus quadratiques et l'autre non :

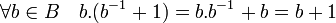
Le polynôme X + 1 divise P(X). Notons Q(X) le polynôme défini par :

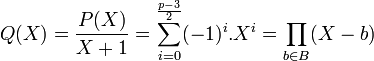
Comme B est de cardinal pair, on obtient :

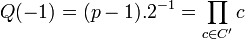
L'élément p - 1 n'est pas un résidu quadratique dans ce cas, et l'inverse de 2 est un résidu quadratique si et seulement si 2 l'est. En conséquence, 2 est un résidu quadratique si le produit des éléments de C ne l'est pas et réciproquement.

C contient exactement 4.n +(r - 3)/2 éléments, donc si r est égal à 3, C contient 2.n résidus non quadratiques le produit des éléments de C est quadratique, donc 2 ne l'est pas. Si r est égal à 7, C contient 2.n + 1 résidus non quadratiques et le produit des éléments de C n'est pas quadratique, donc 2 l'est, ce qui termine l'analyse des différents cas.