Marge d'erreur - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En statistiques, la marge d'erreur est une estimation de l'étendue que les résultats d'un sondage peuvent avoir si l'on recommence l'enquête. Plus la marge d'erreur est importante, moins on peut avoir confiance que les résultats du sondage sont proches des vrais résultats, et ainsi, de la réalité.
La marge d'erreur peut être calculée directement à partir de la taille de l'échantillon (par exemple, le nombre de personnes sondées) et est habituellement reportée par l'un des trois différents niveaux de l'intervalle de confiance. Le niveau de 99% est le plus prudent, le niveau de 95% est le plus répandu, et le niveau de 90% est rarement utilisé. Pour un niveau de confiance de 99%, on est sûr à 99% que la vraie valeur se trouve dans la marge d'erreur de la valeur issue du sondage.
La marge d'erreur prend uniquement en compte l'erreur de l'échantillon. Elle ne prend pas en compte les autres sources potentielles d'erreurs, notamment, le biais dans les questions ou dans l'exclusion d'un groupe n'étant pas questionné, le fait que certaines personnes ne veulent pas répondre, le fait que certaines personnes mentent, les erreurs de calculs.
Calculs
La marge d'erreur est une simple reformulation de la taille de l'échantillon, N. Les numérateurs des équations suivantes sont arrondies à la deuxième décimale.
- Marge d'erreur à 99%
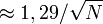
- Marge d'erreur à 95%
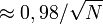
- Marge d'erreur à 90%
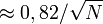
La marge d'erreur n'est pas complètement définie si l'intervalle de confiance n'est pas rapporté. Si un article à propos d'un sondage ne donne pas l'intervalle de confiance, la marge d'erreur peut être approximée pour le degré de confiance désiré à l'aide de la taille de l'échantillon. De plus, si la marge d'erreur à 95% est donnée, il est possible de calculer la marge d'erreur à 99% en l'augmentant d'environ 30%.
Comparaison des pourcentages
Tables
La marge d'erreur est fréquemment utilisée d'une mauvaise façon pour déterminer si un pourcentage est supérieur à un autre. La statistiques qui doit être utilisé dans ce cas est simplement la probabilité qu'un pourcentage soit supérieur à un autre. Le tableau ci-dessous présente les « probability of leading » de deux candidats, en l'absence d'autres candidats, et en prenant un niveau de 95 % de confiance:
| Différence de pourcentages : | 0% | 1% | 2% | 3% | 4% | 5% | 6% | 7% | 8% | 9% | 10% |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1% marge d'erreur | 50.0 | 83.6 | 97.5 | 99.8 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| 2% marge d'erreur | 50.0 | 68.8 | 83.7 | 92.9 | 97.5 | 99.3 | 99.8 | 100 | 100 | 100 | 100 |
| 3% marge d'erreur | 50.0 | 62.8 | 74.3 | 83.7 | 90.5 | 94.9 | 97.5 | 98.9 | 99.6 | 99.8 | 99.9 |
| 4% marge d'erreur | 50.0 | 59.7 | 68.8 | 76.9 | 83.7 | 89.0 | 93.0 | 95.7 | 97.5 | 98.7 | 99.3 |
| 5% marge d'erreur | 50.0 | 57.8 | 65.2 | 72.2 | 78.4 | 83.7 | 88.1 | 91.5 | 94.2 | 96.2 | 97.6 |
| 6% marge d'erreur | 50.0 | 56.5 | 62.8 | 68.8 | 74.3 | 79.3 | 83.7 | 87.4 | 90.5 | 93.0 | 95.0 |
| 7% marge d'erreur | 50.0 | 55.6 | 61.0 | 66.3 | 71.2 | 75.8 | 80.0 | 83.7 | 86.9 | 89.7 | 92.0 |
| 8% marge d'erreur | 50.0 | 54.9 | 59.7 | 64.3 | 68.8 | 73.0 | 76.9 | 80.5 | 83.7 | 86.6 | 89.1 |
| 9% marge d'erreur | 50.0 | 54.3 | 58.6 | 62.8 | 66.9 | 70.7 | 74.4 | 77.8 | 80.9 | 83.7 | 86.3 |
| 10% marge d'erreur | 50.0 | 53.9 | 57.8 | 61.6 | 65.3 | 68.8 | 72.2 | 75.4 | 78.4 | 81.2 | 83.8 |
Par exemple, la probabilité que John Kerry gagne face à Georges Bush selon les données du sondage de Newsweek (une différence de 2% et une marge d'erreur de 4%) est d'environ 68,8%, à condition qu'ils aient utilisé un niveau de 95% de confiance. Voici la même table pour un niveau de 99% de confiance:
| Différence de pourcentages : | 0% | 1% | 2% | 3% | 4% | 5% | 6% | 7% | 8% | 9% | 10% |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1% marge d'erreur | 50.0 | 90.1 | 99.5 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| 2% marge d'erreur | 50.0 | 74.1 | 90.2 | 97.4 | 99.5 | 99.9 | 100 | 100 | 100 | 100 | 100 |
| 3% marge d'erreur | 50.0 | 66.6 | 80.5 | 90.2 | 95.7 | 98.4 | 99.5 | 99.9 | 100 | 100 | 100 |
| 4% marge d'erreur | 50.0 | 62.6 | 74.1 | 83.3 | 90.2 | 94.7 | 97.4 | 98.8 | 99.5 | 99.8 | 99.9 |
| 5% marge d'erreur | 50.0 | 60.2 | 69.7 | 78.1 | 84.9 | 90.2 | 94.0 | 96.5 | 98.1 | 99.0 | 99.5 |
| 6% marge d'erreur | 50.0 | 58.5 | 66.6 | 74.1 | 80.5 | 85.9 | 90.2 | 93.4 | 95.8 | 97.4 | 98.5 |
| 7% marge d'erreur | 50.0 | 57.3 | 64.4 | 71.0 | 77.0 | 82.2 | 86.6 | 90.2 | 93.0 | 95.2 | 96.8 |
| 8% marge d'erreur | 50.0 | 56.4 | 62.6 | 68.6 | 74.1 | 79.0 | 83.4 | 87.1 | 90.2 | 92.7 | 94.7 |
| 9% marge d'erreur | 50.0 | 55.7 | 61.3 | 66.6 | 71.7 | 76.3 | 80.6 | 84.3 | 87.5 | 90.2 | 92.5 |
| 10% marge d'erreur | 50.0 | 55.1 | 60.2 | 65.1 | 69.7 | 74.1 | 78.1 | 81.7 | 85.0 | 87.8 | 90.3 |
Si le sondage réalisé pour Newsweek utilise un niveau de 99% de confiance, alors la probabilité que Kerry gagne face à Bush serait de 74,1%. Dès lors, il semble évident que le niveau de confiance a un impact significatif sur la probabilité de gagner.

















































