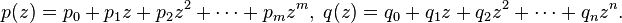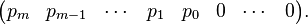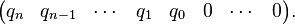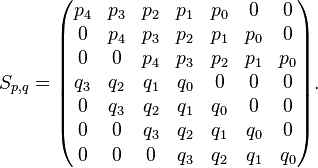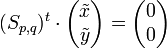Matrice de Sylvester - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En algèbre linéaire, la matrice de Sylvester de deux polynômes apporte des informations d'ordre arithmétique sur ces polynômes. Elle tient son nom de James Joseph Sylvester. Elle sert à la définition du résultant de deux polynômes.
Définition
Soient p et q deux polynômes non nuls, de degrés respectifs m et n.
La matrice de Sylvester associée à p et q est la matrice carrée
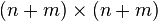
- la première ligne est formée des coefficients de p, suivis de 0
- la seconde ligne s'obtient à partir de la première par permutation circulaire vers la droite
- les (n-2) lignes suivantes s'obtiennent en répétant même opération
- la ligne (n+1) est formée des coefficients de q, suivis de 0
- les (m-1) lignes suivantes sont formées par des permutations circulaires
Ainsi dans le cas m=4 et n=3, la matrice obtenue est
Le déterminant de la matrice de p et q est appelé déterminant de Sylvester ou résultant de p et q.
Applications
L'équation de Bézout d'inconnues les polynômes x (de degré <n) et y (de degré <m)
peut être réécrite matriciellement
dans laquelle t désigne la transposée,
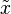
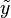
Ainsi le noyau de la matrice de Sylvester donne toutes les solutions de cette équation de Bézout avec degx < degq et degy < degp.
Le rang de la matrice de Sylvester est donc relié au degré du PGCD de p et q.
-
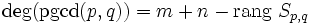
Notamment, le résultant de p et q est nul si et seulement si p et q ont un facteur commun de degré supérieur ou égal à un.