Modèle de Gompertz - Définition
La liste des auteurs de cet article est disponible ici.
Modèle de Gompertz et dynamique des populations
La loi de Gompertz-Makeham décrit la dynamique de la mortalité, qui appartient à la dynamique des populations.
Le modèle a surtout été utilisé pour représenter la croissance de certains organismes.
Il permet de rendre compte de la relation d'allométrie entre 2 variables, en plus de la bonne représentation qu'il offre pour une variable.
Lorsque l'on compare le modèle de Gompertz au modèle de Verhulst, on observe un comportement similaire (croissance exponentielle de la population) néanmoins dans le cas du modèle de Gompertz, elle est plus rapide. Ces deux modèles sont concurrents pour la modélisation de la croissance des organismes.
Le modèle mathématique de Gompertz
Le modèle de Gompertz permet de modéliser la croissance d'une population régulée.
On l'exprime ainsi sous forme d'équation différentielle :
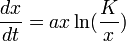
Il est également exprimé sous sa forme intégrée :
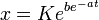
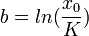
La forme intégrée du modèle de Gompertz est souvent utilisée pour le calcul numérique, tandis que la forme différentielle se prête mieux à l'interprétation.
Les paramètres :
- x représente la biomasse (taille, masse corporelle…)
- t le temps
- K la capacité limite du milieu
- a une constante
Point d'équilibre du modèle
Un état d'équilibre de la population est observé quand la population n'évolue pas. Les points d'équilibre sont les valeurs x * pours lesquelles
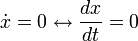
On trouve deux points d'équilibre
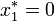
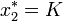
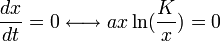
Deux solutions possibles:
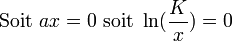
- Pour le premier point :
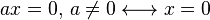
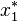
- Pour le deuxième point :
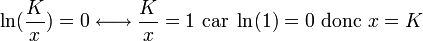
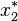
Stabilité Locale
On étudie la stabilité au point d'équilibre
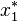
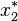
On observe le signe de
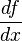
Si  alors x* est instable.
alors x* est instable.
Si
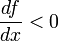
Pour cela, on calcule la dérivée partielle en ces points :
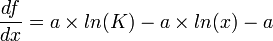
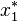
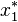
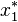
Au point d'équilibre
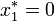
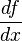
 est instable .
est instable .
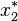
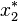
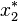
Au point d'équilibre
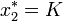
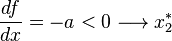
Voir également
Liens Internes
- Allométrie
- Croissance exponentielle
- Dynamique des populations
- Modèle de Verhulst
Liens Externes
Herman Denis, « MESURE DE LA LONGÉVITÉ DES ANIMAUX ET DES ÊTRES HUMAINS »
Références
- (en) James Dickson Murray, Mathematical Biology: Spatial models and Biomedical Applications, t. II, Springer, 3e éd., 811 p.
- Graziella Caselli, Démographie : Analyse et synthèse : Population et société, vol. VI, Institut National d'Etudes Démographiques, 585 p.
- Graziella Caselli, Démographie : Analyse et synthèse : Les déterminants de la mortalité, vol. III, Institut National d'Etudes Démographiques, 2002, 483 p.
- Alain Branger, Microbiochimie et alimentation, Educagri, 344 p. , p. 113-114

















































