Modèle de Gompertz - Définition

Introduction

Le modèle de Gompertz (ou loi de mortalité de Gompertz-Makeham) établit que le taux de mortalité est la somme de termes indépendants de l'âge (termes de Makeham) et de termes dépendants de l'âge (fonction de Gompertz).

Ce modèle suggère également la diminution exponentielle du nombre d'organismes vivants proportionnellement à l'augmentation linéaire de l'âge.

Histoire

La mathématisation de la science de la population progresse au XIXe siècle, notamment grâce à la loi de la mortalité établie par Benjamin Gompertz. Mais également grâce à la loi logistique de Pierre François Verhulst, selon laquelle la croissance de la population ralentit.

En effet en 1825, Benjamin Gompertz propose que la force de mortalité augmente de façon exponentielle avec l'âge comme suit :

μ_x = Bc^x où B et c sont des constantes.

Cependant, se pose le problème de prendre en compte les causes de décès qui ne seraient pas directement liées à l'âge.

C'est ainsi que William Makeham propose d'extrapoler la force de mortalité aux grands âges sur la base d'une loi de Gompertz modifiée et tenant compte des causes de décès indépendantes de l'âge:

μ_x = A + Bc^x où A est le risque de mourir pour l'ensembles des causes indépendantes de l'âge.

Dans des conditions où les causes externes de décès sont rares, les termes qui ne dépendent pas de l'âge sont souvent négligeables. On parle alors de la loi de Gompertz, due à Benjamin Gompertz en 1825.

Le modèle est largement utilisé en démographie et gérontologie pour des prévisions adéquates du taux de mortalité chez certaines espèces (non humaines) et pour comparer les taux de vieillissement actuariels entre et parmi différentes espèces.

Il représente bien la croissance de certaines variables morphologiques (taille, masse corporelle...) d'organismes supérieurs (voir exemple d'application sur la croissance en masse corporelle du rat musqué en fonction de son âge.)

Quelques exemples d'applications

• Applications en microbiochimie et alimentation pour décrire les phases de croissance microbienne (voir : ISBN 978-2-84444-558-2)

• Applications dans des modèles de prédictions de croissance

Modélisation de la croissance pour le rat musqué

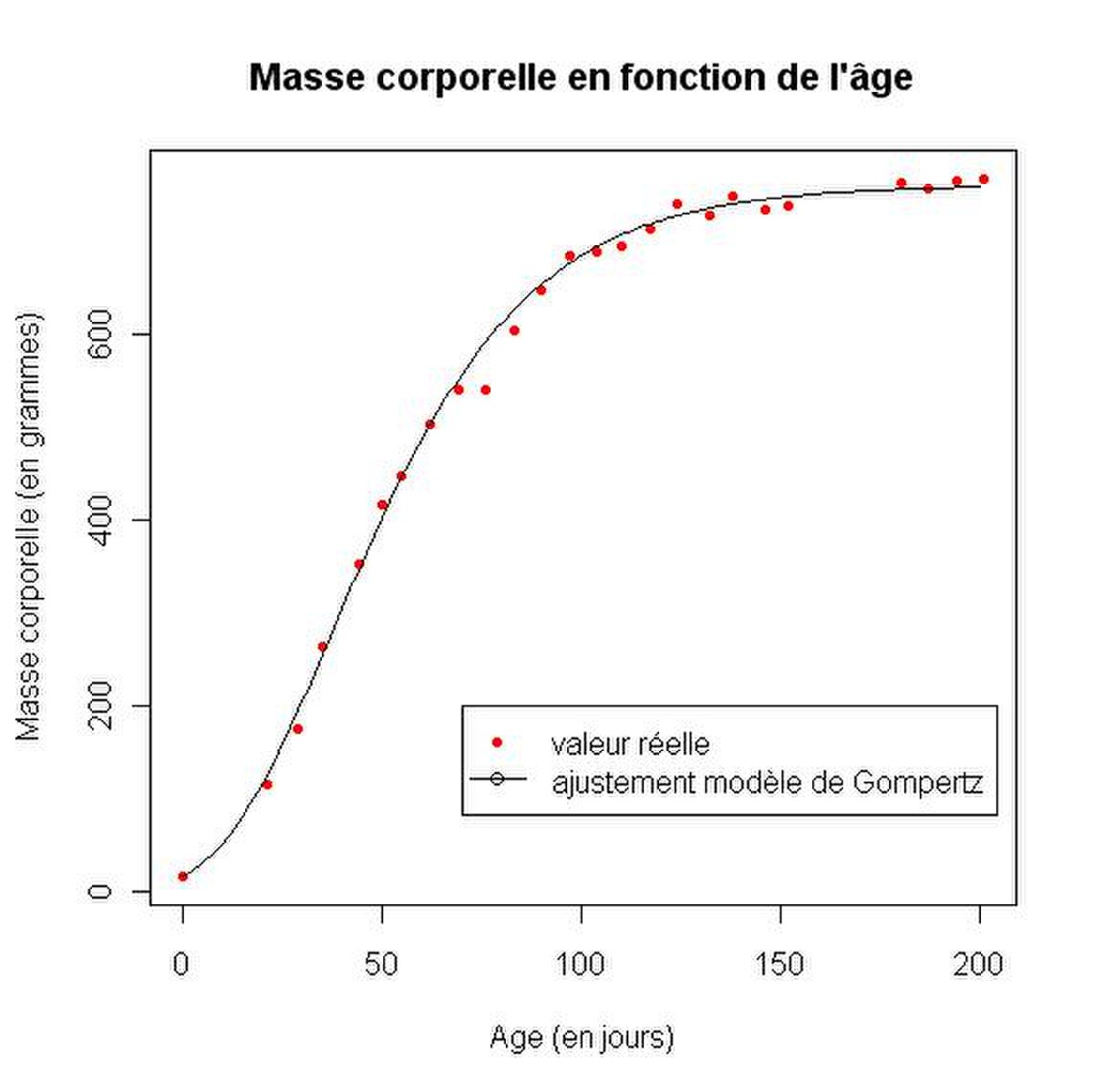
Le modèle de Gompertz représente bien la croissance en masse corporelle du rat musqué ou sa taille en fonction de son âge.

Ajustement du modèle de Gompertz aux données sur la masse corporelle avec x₀ = 16, a = 0.036 et K = 760.

L'équation s'écrit donc

Exemple de représentation de données et ajustement au modèle de Gompertz.

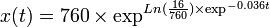
      a=0.036      K=760      x0=16      t=seq(0, 200, by =1)      x = K*exp(log(x0/K) * exp(-a*t))            #data      age=c(0,21,29,35,44,50,55,62,69,76,83,90,97,104,110,117,124,132,138,146,152,180,187,194,201)      masse=c(16,116,175,264,352,416,447,503,540,540,603,646,684,688,695,712,739,728,747,733,738,763,757,765,767)            #graphics      plot(age,masse,type="p",pch=20,col="red",main="Masse corporelle en fonction de l'âge",ylab="Masse corporelle (en grammes)",xlab="Age (en jours)")      lines(t,x, type="l",pch=1)      legend(70,200,c("valeur réelle","ajustement modèle de Gompertz"),lty=c(0,1),pch=c(20,1),col=c("red","black"))      

Modélisation de la croissance des tumeurs

La courbe de Gompertz est utilisée pour ajuster les données de la croissance des tumeurs. En fait, les tumeurs sont des populations de cellules dans un espace confiné où la disponibilité des éléments nutritifs est limitée. En notant la taille de la tumeur X (t), il est utile d'écrire la courbe de Gompertz comme suit:

où

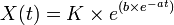
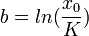
X (0) est la taille de la tumeur au moment de l'observation de départ. K est la taille maximale qui peut être atteinte avec les éléments nutritifs disponibles, c’est-à-dire la population asymptotique de cellules tumorales.