Pavage de Penrose - Définition

Pavage avec des losanges (pavage de type 3)

Assemblage de losanges dans un pavage de Penrose

Il est aussi possible de paver le plan à l'aide de deux figures géométriques simples comme les deux losanges suivants. À condition de les assembler en respectant la couleur et le sens des vecteurs. Ces contraintes d'assemblage assurent que le pavage obtenu ne sera pas périodique. Comme précédemment, il existe une infinité de pavages du plan non périodiques à l'aide de ces deux pièces.

Découpe des losanges

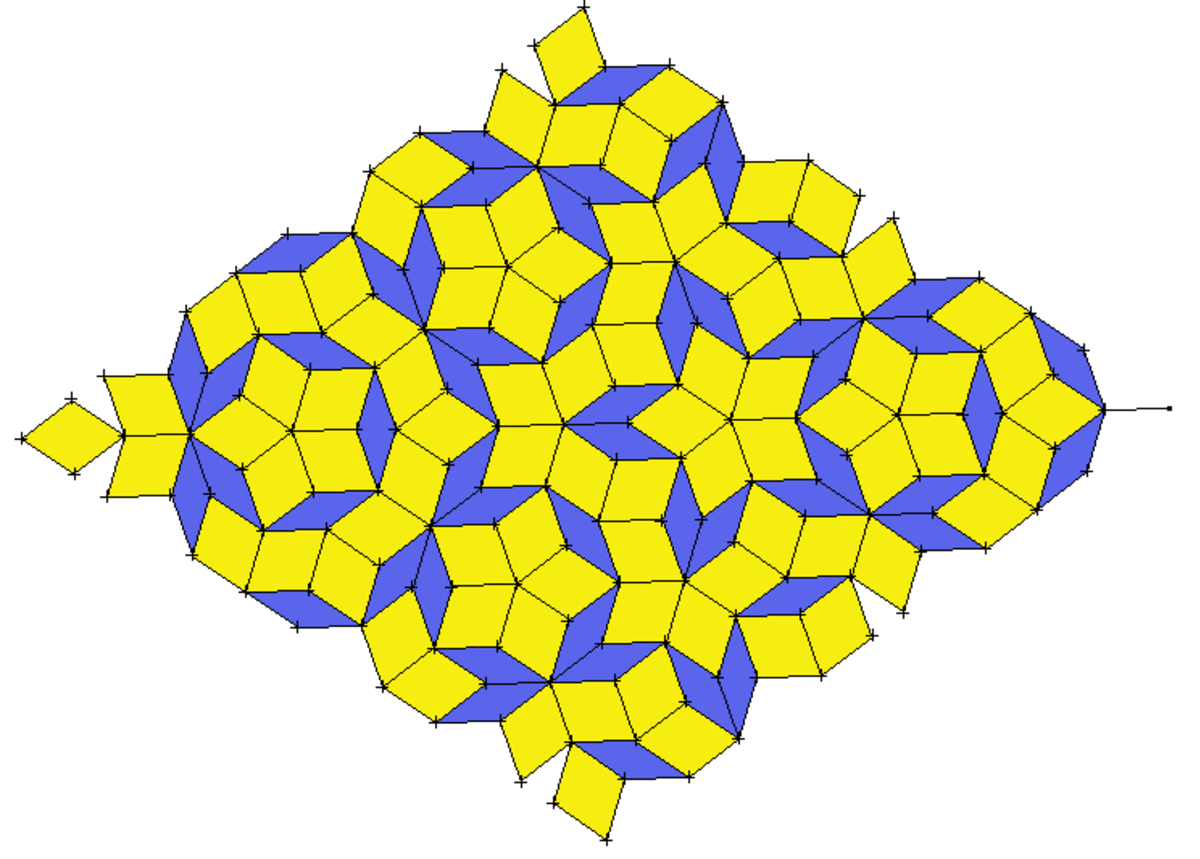
Comme pour les autres types de pavage de Penrose, on peut définir aussi un algorithme de "construction par découpage" : il suffit de découper chaque gros losange en un gros losange, deux demi-losanges fins et deux demi-losange gros, et chaque losange fin en deux demi-losange fins et deux demi-losanges gros. La cohérence du procédé est assurée par le fait que les demi-losanges ainsi générés s'associent toujours avec leur voisin pour reconstituer un losange complet (ce qui assure la disparition des lignes en pointillé visibles sur la figure ci-contre).

Pavage en losanges

La figure obtenue au bout de plusieurs itérations laisse déceler une quasi-symétrie d'ordre 5. Il est facile de prouver que, comme pour les triangles d'or, la proportion entre le nombre de gros losanges et celui de losanges fins tend vers le nombre d'or φ. Ce qui assure que le pavage ainsi construit n'est pas périodique.

Pavage avec cerfs-volants et fléchettes (pavage de type 2)

Le pavage précédent a l'avantage de la simplicité mais sa construction n'est pas unique : en effet, chaque découpage d'un triangle peut s'effectuer d'au moins deux façons différentes (symétriques). En outre, ces découpages ne donnent pas une impression de régularité et conduisent donc à des pavages assez peu élégants.

Mais on peut concevoir un autre type de pavage.

Cerf-volant et fléchette

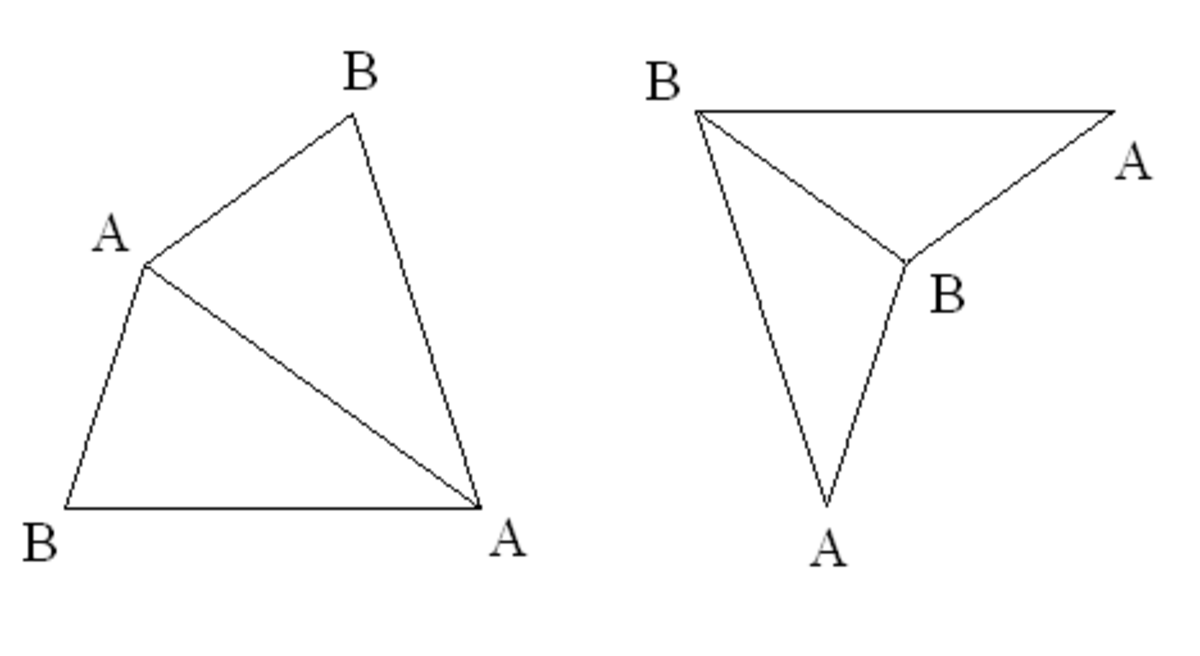
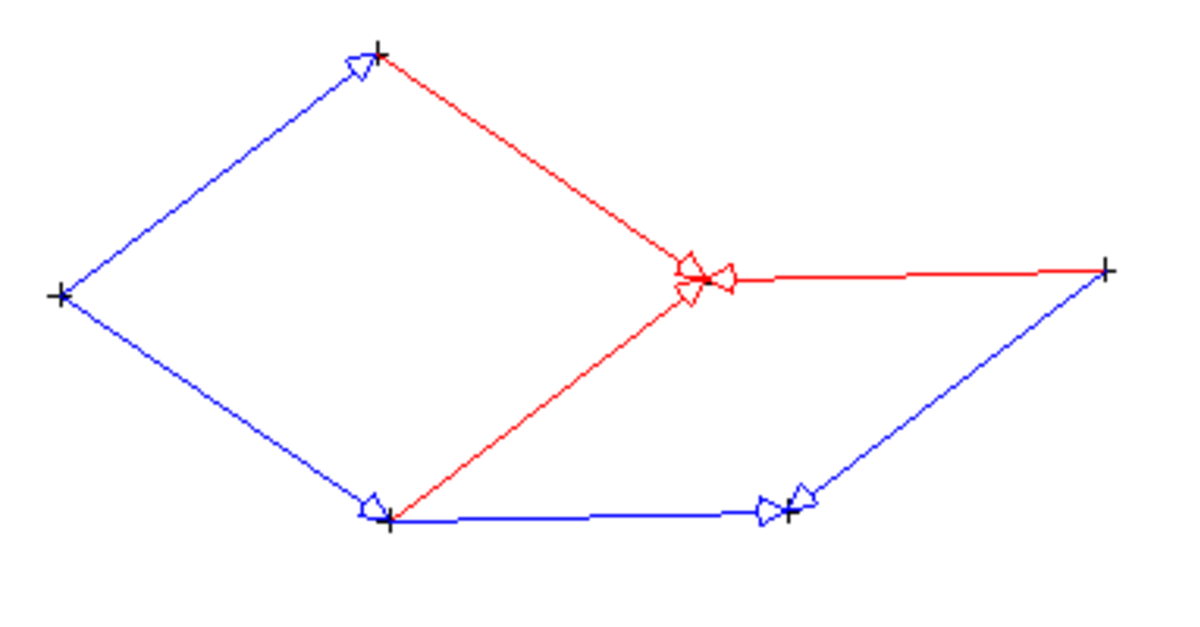
En réunissant deux triangles d'or aigus ayant pour sommet commun le sommet dont la bissectrice est un axe de symétrie pour les deux autres sommets (sommets correspondants à un angle de 36°), on obtient un "pavé" en forme de cerf-volant. Si on fait la même construction avec deux triangles obtus (sommets correspondants à un angle de 108°), on obtient un "pavé" en forme de fléchette.

On peut alors paver le plan avec ces deux nouveaux "pavés". En effet, si on prend bien soin de ne jamais accoler une flèchette et un cerf-volant en formant un parallélogramme, on peut construire ainsi un pavage non périodique. Il suffit pour cela de nommer les sommets comme indiqué sur la figure ci-dessus et de se fixer pour règle de n'accoler deux sommets que s'ils portent le même nom. Il existe une infinité de pavages du plan de ce type.

Découpes du cerf volant et de la fléchette

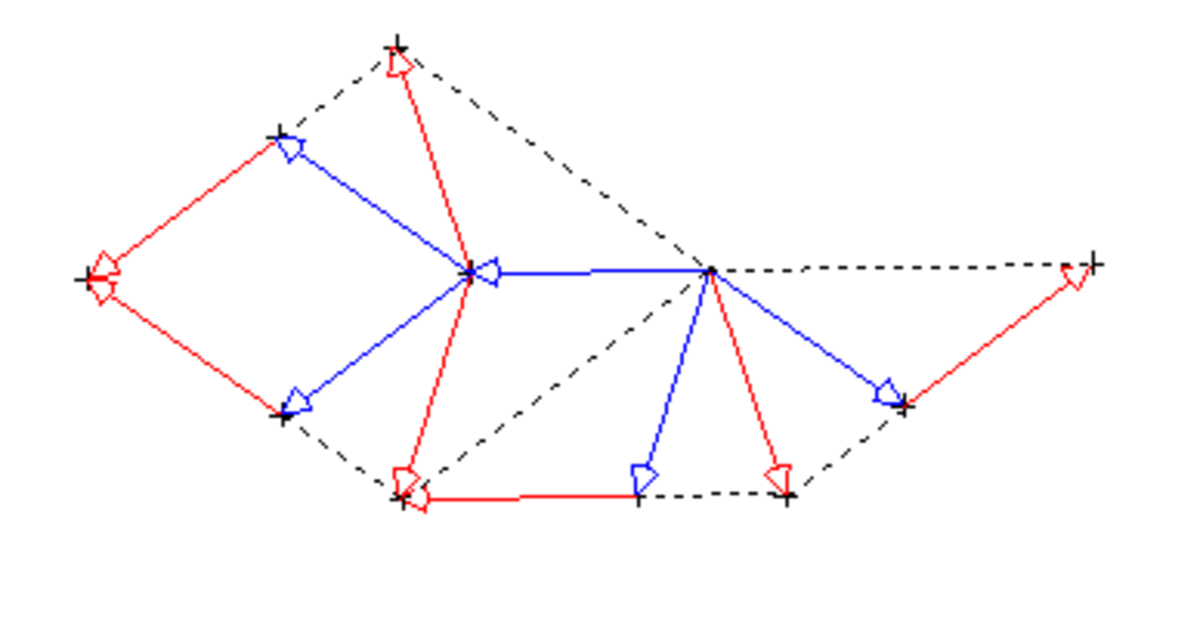
Mais on peut également, comme pour le pavage à l'aide des triangles d'or, définir un algorithme de "construction par découpage" consistant à chaque étape à découper chaque cerf-volant en deux cerfs-volants et deux demi fléchettes et une fléchette en un cerf-volant et deux demi-fléchettes, et en agrandissant d'un facteur φ le résultat obtenu (remarquer que les sommets changent de nom à chaque étape, A devenant B et B devenant A).

La cohérence du procédé est assurée par le fait que les demi-fléchettes ainsi générées s'associent toujours avec leur voisine pour reconstituer une fléchette complète (ce qui assure la disparition des lignes en pointillé visibles sur la figure précédente).

Pavage de Penrose avec cerfs-volants et fléchettes

La figure obtenue au bout de plusieurs itérations laisse déceler une quasi-symétrie d'ordre 5. Il est facile de prouver que, comme pour les triangles d'or, la proportion entre le nombre de cerfs-volants et celui de fléchettes tend vers le nombre d'or φ, ce qui assure que le pavage ainsi construit n'est pas périodique.

A la différence du premier type de pavage, ici la construction par découpage génère un seul type de pavage de type 2 puisque le découpage des cerfs-volants et des fléchettes ne peut être réalisé que d'une seule façon !

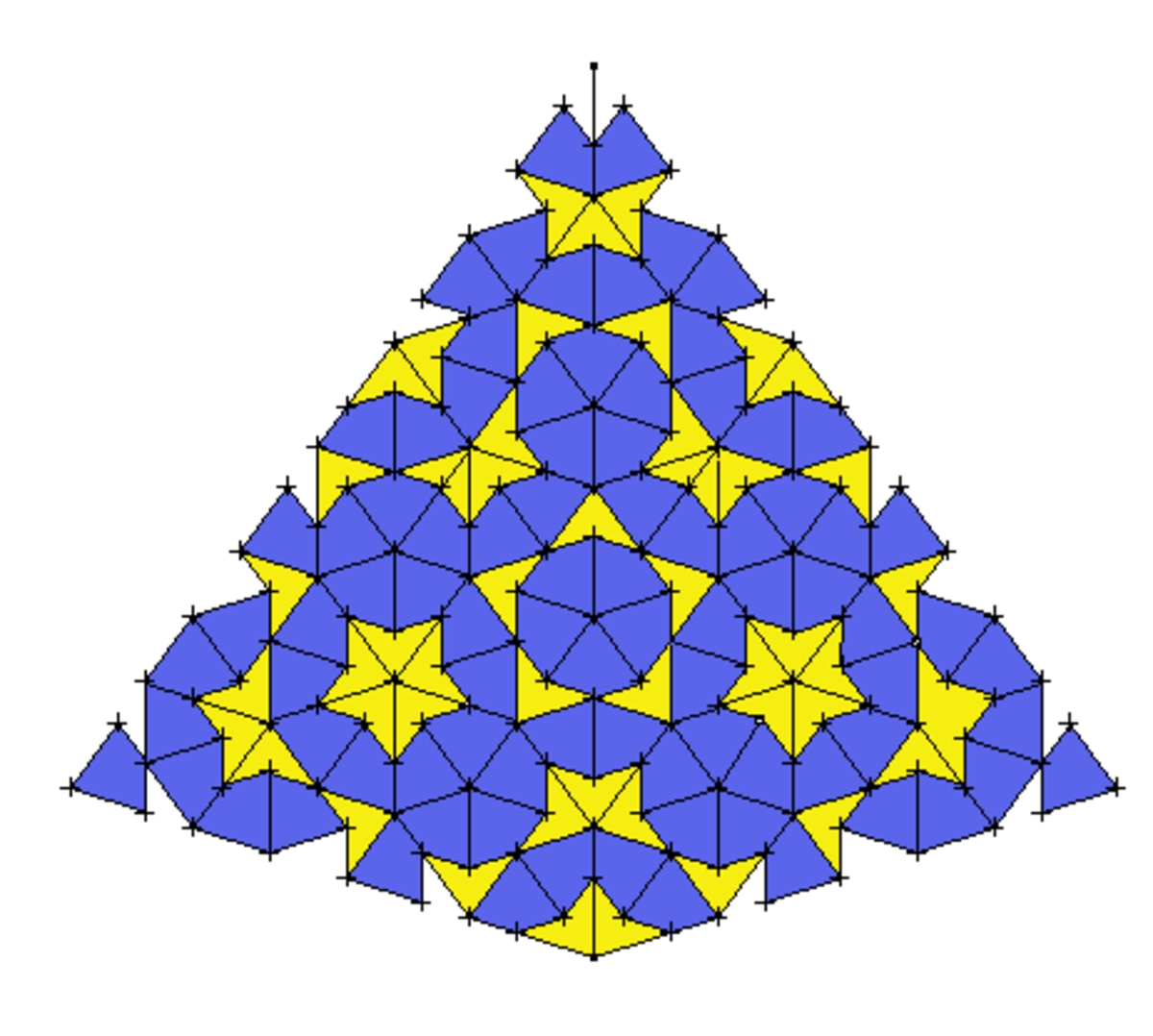
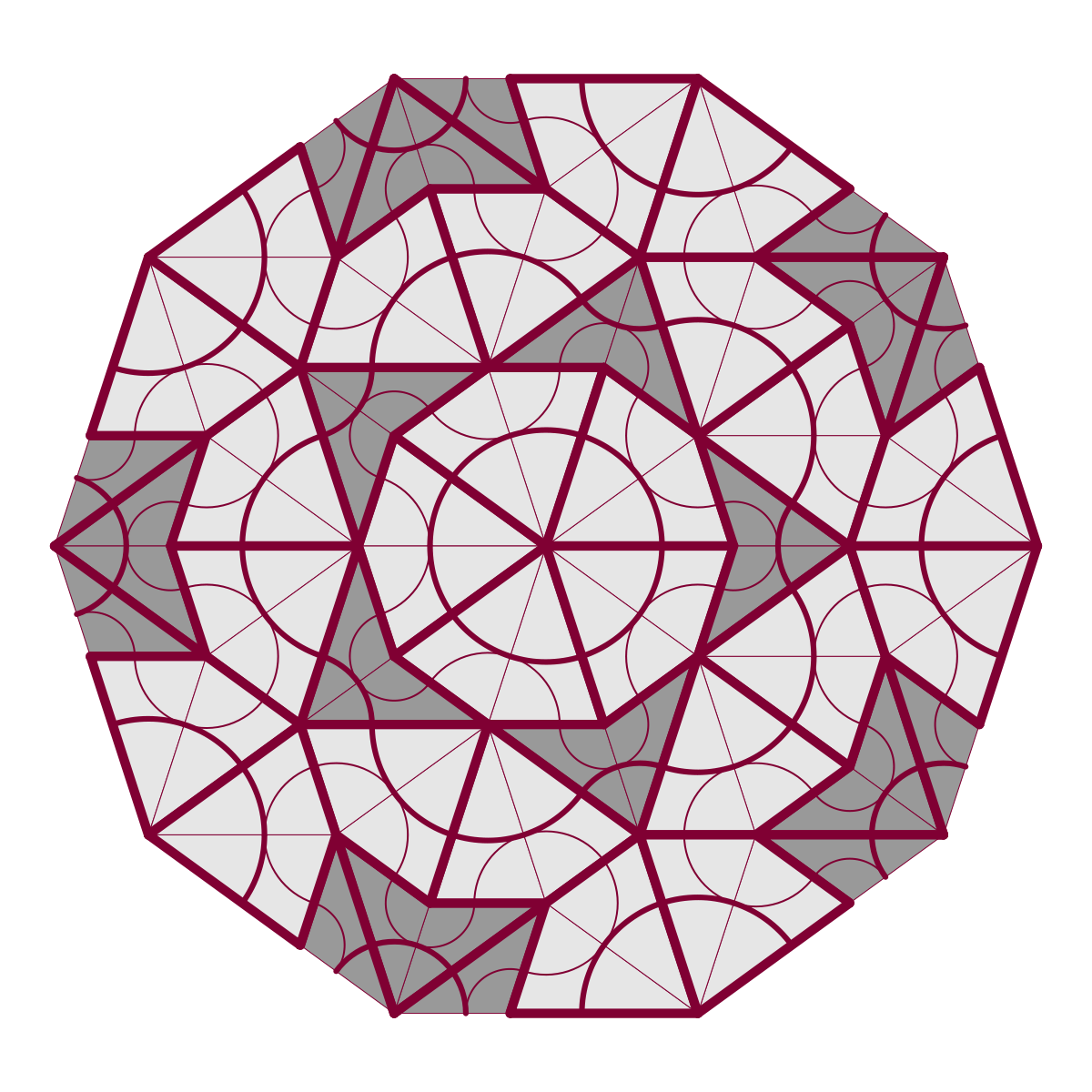
Un exemple : trois générations de 4 figures

Voici des exemples de générations successives en partant d'une forme de base. Dans les figures « Soleil » et « Étoile », on retrouve la figure de départ réduite à la deuxième génération. Le « Soleil » apparaît même dans la génération 3.

Nom	Generation 0	Generation 1	Generation 2	Generation 3
Cerf-volant (demi)
Flèche (demie)
Soleil
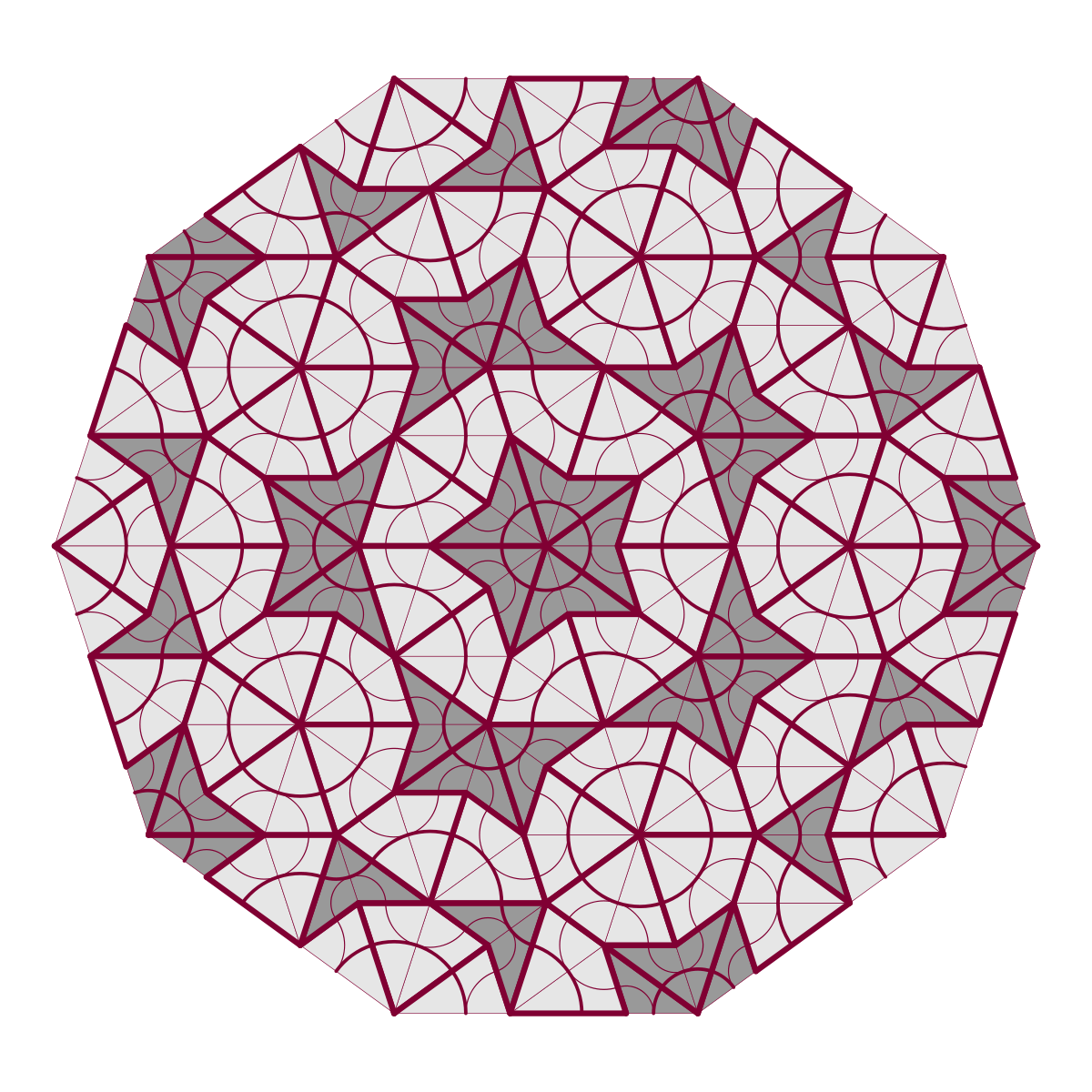
Étoile