Pavage de Penrose - Définition

Introduction

Les pavages de Penrose sont des pavages du plan découverts par le mathématicien et physicien britannique Roger Penrose dans les années 1970. Ce sont des pavages non périodiques caractérisables par des règles locales : s'ils ne sont historiquement pas les premiers à vérifier cette propriété, ils sont parmi les plus simples, et à ce titre largement étudiés (le premier tel pavage, construit par Robert Berger en 1966, comportait 20426 tuiles).

Les 17 pavages périodiques du plan étaient connus de longue date quand Roger Penrose s'est intéressé aux pavages non périodiques. Son intention n'était pas d'ouvrir un nouveau champ des mathématiques et de la physique mais seulement de créer un divertissement mathématique. En 1974, il publia un article présentant un pavage du plan à l'aide de pentagones, de losanges, de pentagrammes et de portions de pentagrammes.

Les pavages de Penrose présentent une symétrie d'ordre 5 (invariance par rotation d'angle 2π/5 radian, soit 72 degrés). Ils ne sont pas périodiques, c'est-à-dire qu'on ne peut les décrire comme un motif répété sur une grille régulière. Ils sont cependant quasi-périodiques, c'est-à-dire que tout motif apparaissant dans le pavage réapparaît régulièrement.

Les pavages de Penrose ne seraient restés qu'un joli divertissement mathématique si n'avaient été découverts, en 1984, des matériaux présentant une structure fortement ordonnée comme celle des cristaux mais non périodique : les quasi-cristaux. Les pavages non périodiques, en particulier ceux de Penrose, s'avèrèrent alors un modèle plausible de ces étranges matériaux.

Il existe trois types de pavages de Penrose, chacun comportant une infinité de variantes :

• Le , qu'on appelle P1, utilise comme pièces de base des pentagones, des losanges, des pentagrammes et des portions de pentagramme.
• Le , ou P2, a pour pièces de base deux quadrilatères, l'un convexe, l'autre concave, connus comme « cerfs-volants » et « fléchettes ».
• Le , P3, a pour pièces de base deux sortes de losanges, « fins » et « gros ».

On s'est aperçu que fléchettes, cerfs-volants et losanges peuvent tous être construits à partir d'un paire de triangles d'or. Les pièces de P2, « cerfs-volants » et « fléchettes », sont obtenues respectivement par le collage de deux triangles d'or aigus de côtés proportionnels à [1;φ;φ] et par le collage de deux triangles d'or obtus de côtés proportionnels à [1;1;φ]. Celles de P3, les losanges fins et gros, par le collage de deux triangles d'or aigus de côtés proportionnels à [1;φ;φ] et par le collage de deux triangles d'or obtus de côtés proportionnels à [φ;φ;φ²]. Cette série de simplifications permet de considérer les triangles d'or comme prototypes des autres pièces et de dire qu'un précède les autres.

Pavage de Penrose avec triangles d'or (pavage de type 0)

Il existe de nombreuses façons de définir un triangle d'or. L'une des plus simples est la suivante :
"Un triangle d'or est un triangle isocèle possédant la propriété suivante : pouvoir être découpé en 2 triangles isocèles inégaux et possédant à leur tour la propriété "

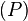
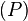
On peut démontrer qu'il n'existe que deux types de triangles d'or, le type aigu (A) et le type obtus (O). ces deux types de triangles d'or pouvant s'obtenir en découpant un pentagone régulier de la façon suivante :

Chacun de ces types possède un angle de 36 ° (soit radians). les deux autres angles étant (comme le montre la figure ci-dessus), soit égaux à , soit multiples de (d'un facteur 2 ou 3).

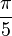
L'angle est lié au nombre d'or φ par de nombreuses propriétés ; en effet :

• et
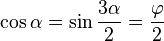
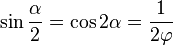
• Les côtés d'un triangle d'or aigu ont des longueurs proportionnelles à [1;φ;φ]
• Les côtés d'un triangle d'or obtus ont des longueurs proportionnelles à [1;1;φ]

La propriété peut être précisée de la façon suivante :

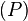
• Tout triangle d'or aigu (A) de dimensions [1; φ; φ] peut se décomposer (de 4 façons différentes, 2 à 2 symétriques) en 3 triangles : un triangle d'or obtus [1/φ; 1/φ; 1] et deux triangles d'or aigus [1/φ; 1 ;1], ces nouveaux triangles ayant donc, par rapport au triangle d'or générateur, une taille divisée par φ ;
• Tout triangle d'or obtus (O) de dimensions [1; 1; φ] peut se décomposer (de 2 façons différentes et symétriques) en deux triangles : un triangle d'or aigu [1/φ; 1; 1] et un triangle d'or obtus [1/φ; 1/φ; 1].

Animation montrant comment on peut, avec des triangles d'or, réaliser un pavage de Penrose de type 0 (6 étapes)
(toutefois, l'agrandissement dont il est question dans le texte ci-contre n'a pas été réalisé, afin d'améliorer la visibilité !)

Ainsi précisée, la propriété peut être utilisée pour construire un pavage de Penrose de type 0. Voici comment :

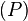
En découpant un premier triangle d'or (aigu ou obtus, peu importe) et en opérant un agrandissement d'un facteur φ, puis en recommençant l'opération précédente une infinité de fois, on constitue un pavage complet du plan à l'aide des deux types de triangles d'or. Si, à l'étape n, on appelle le nombre de triangles aigus et le nombre de triangle obtus, on observe les formules de récurrence :

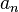
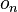
o_{n + 1} = o_n + a_n

a_{n + 1} = o_n + 2a_n = o_{n + 1} + a_n

En considérant la suite u_n définie par

u_2n = o_n

u_{2n + 1} = a_n,

on s'aperçoit que cette suite vérifie la relation de récurrence de la suite de Fibonacci

u_{n + 2} = u_{n + 1} + u_n,

suite dont on sait que le rapport de deux termes consécutifs tend vers le nombre d'or φ. Ainsi la valeur limite du rapport du nombre de triangles obtus et du nombre de triangles aigus est un nombre irrationnel, ce qui entraîne que le pavage obtenu de cette façon ne peut pas être périodique.