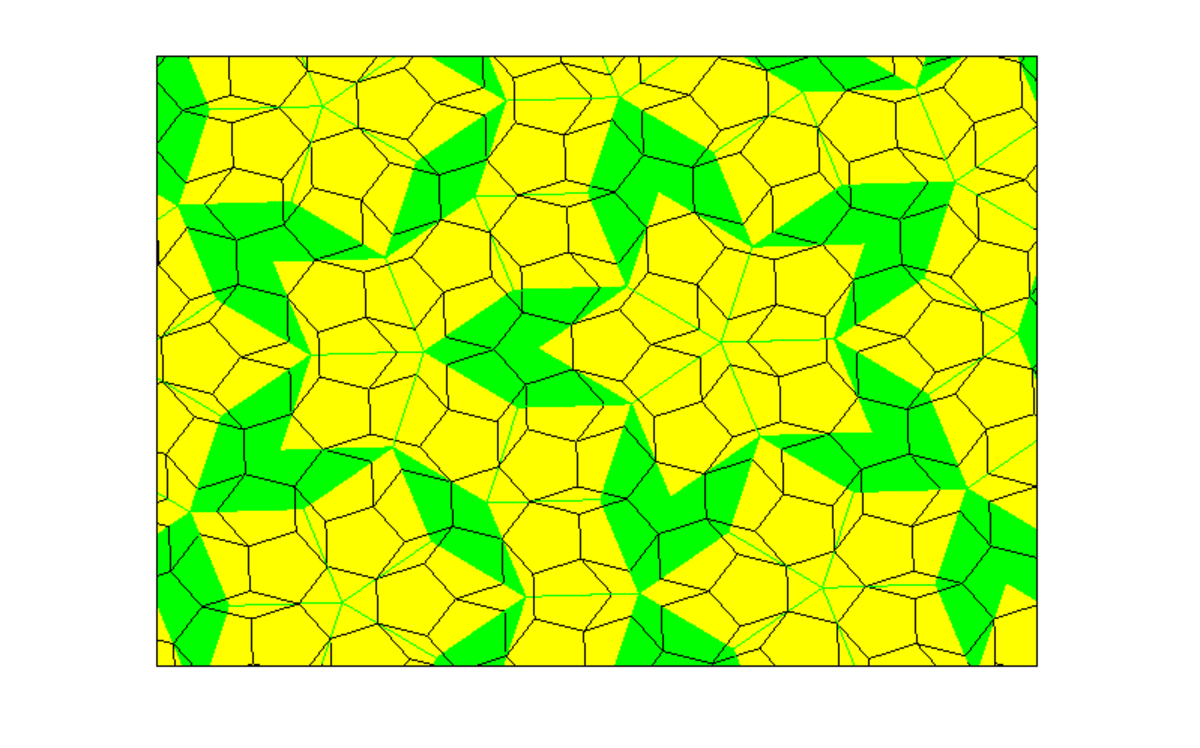
Pavage de Penrose - Définition
La liste des auteurs de cet article est disponible ici.
Recouvrement avec des décagones
La mathématicienne allemande Petra Gummelt a prouvé en 1996 qu'un pavage de Penrose pouvait être obtenu en recouvrant le plan uniquement avec des décagones, à condition toutefois que deux types discrets d'empiètement soient permis. Le décagone proposé est décoré avec cinq cerf volants et l'empiètement permis ne change pas la configuration de ces parties coloriées.
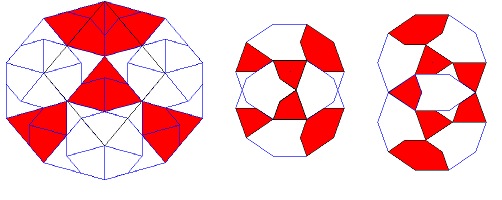
Il est possible de décomposer le décagone en fléchettes et cerfs volants, réduisant le tableau obtenu en un pavage de Penrose. Le pavage avec des losanges peut être retrouvé directement en gravant un gros losange dans le décagone; les parties laissées en creux seront celles que remplissent les losanges fins. Cette nouvelle facon de procéder a eu un impact considérable sur les conceptions à propos de la formation des quasicristaux.
Pavage dit 'pentagonal' (pavage de type 1)
Le pavage construit autour de pentagones, P1, est en fait le premier découvert par Penrose, qui s'est inspiré d'abord des recherches de Johannes Kepler. Il est bien connu qu' on ne peut couvrir le plan avec des pentagones, mais trois autres pièces suffisent pour combler les interstices, tout en imposant l'ordre apériodique. Ces pièces sont un losange fin, un pentagramme et un 'bateau', qui représente à peu près les 3/5 d'un pentagramme. Pour la construction directe du pavage apériodique il faut aussi distinguer trois sortes de pentagones. Une solution bien plus simple consiste à esquisser des pentagones sur les losanges fins et gros qu'on arrange en pavage de type 3.
On peut retrouver directement le pavage par triangles d'or dans le pavage pentagonal, sans utiliser les losanges. Si l'on assigne aux pointes des pentagones successivement les nombres 1, 3, 5, 2, 4, tous les points qui définissent le pavage P3 seront numérotés. Cela peut être fait d'une manière consistante et non équivoque en tournant à gauche ou à droite selon les cas. Choisissant les points qui portent un même numéro, on obtient un pavage de . Le sous-ensemble des points numérotés avec 3 et 4 donne une autre variante de pavage de Penrose, obtenue avec deux pièces connues comme 'papillon' et 'navette'.
Bibliographie
- Penrose R., Bull. Inst. Maths. Appl. 10 (1974) 266
- Kepler J., Harmonices Mundi, 1619, [1]
- Lück R., Penrose Sublattices, J. of Non Crystaline Solids 117-8 (90)832-5
- P. Gummelt, Geometriae Dedicata 62, 1 (1996)
- E. Makovicky (1992), 800-year-old pentagonal tiling from Maragha, Iran, and the new varieties of aperiodic tiling it inspired. In: I. Hargittai, editor: Fivefold Symmetry, pp.67-86. World Scientific, Singapore-London
- Lu J., and Steinhardt p., "Decagonal and Quasi-crystalline Tilings in Medieval Islamic Architecture". Science 315 (2007) 1106-1110.
- Luck R., Dürer-Kepler-Penrose the devlopment of pentagonal tilings, Mat. Sci. Eng. 294-6 (2000) 263-7
- Penrose R., U.S. Patent 4,133,152 "Set of tiles for covering a surface," issued January 9, 1979 (expired)
Sources
- L'aventure des pavages de Penrose Revue tangente et la recherche (avril-mai 2000)
Occurrences
On peut rapporter les occurrences du pavage de Penrose à trois grandes catégories:
- Mathématiques: en fait c'est le seul contexte adéquat pour la considération des pavages de Penrose. Étant des objets non finis, la plupart des assertions à leur sujet n'ont de validité qu'avec preuves à l'appui. L'existence d'un ensemble de 'tuiles' apériodique a été démontrée dans les années 1960 et les cas particuliers réduits à deux pièces ont l'avantage d'être parmi les plus simples possibles. Alain Connes a fait des pavages de Penrose un exemple privilégié pour sa géométrie non commutative.
- A un niveau plus élémentaire on a trouvé de multiples et très étroites relations entre le nombre d'or, les suites de Fibonacci et les pavages de Penrose.
- Physique: l'intérêt des physiciens n'est venu qu'après 1984, quand furent découverts les premiers quasicristaux. Assez vite il a été établi que deux types présentent une quasi-symétrie d'ordre 5 : ceux à structure icosaédrique et ceux à structure simplement décagonale. Dans les deux cas il existe des plans où la disposition des atomes donne un pavage de Penrose. Dans leurs travaux les physiciens ont recours à une méthode générale qui permet d'obtenir des pavages non-périodiques à partir de simples grilles dans des dimensions supérieures à 3.
- Art: la valeur esthétique des pavages de Penrose est immédiatement perceptible. On peut supposer que c'est là le même mécanisme psychique qui a amené le développement des entrelacs et autres ornements semblables. Le rapprochement avec les décorations à symétrie centrale d'ordre 5 ou 10 a été fait dès le début de la vogue quasicristalline. À la mosquée de Darb-i Imam à Isfahan on observe des motifs qui ont permis d' affirmer que les artisans de l'Islam médiéval disposaient de tous les éléments pour construire un pavage de Penrose . On trouve des motifs faits avec des pentagones et des losanges parmi les esquisses d' Albert Dürer et qui peuvent être mis en connexion avec le travail de Johannes Kepler. Le fragment de pavage qui figure dans Harmonices Mundi peut être prolongé de façon apériodique, ce qui produit un type équivalent à celui de Penrose (P1). Roger Penrose a homologué sa découverte comme 'un jeu de tuiles pour couvrir des surfaces', en précisant que 'l'arrangement qu'elles forment est nécessairement non-périodique, ce qui lui donne un attrait visuel considérable' et a veillé sur l'utilisation commerciale. Des artistes contemporains (Clark Richert, Jos Leys) se sont inspirés de sa trouvaille géniale.