Polynôme en plusieurs indéterminées - Définition

Introduction

En algèbre, un polynôme en plusieurs indéterminées à coefficients dans un anneau A commutatif unitaire (et souvent intègre) est un élément d'une structure d'algèbre, qui est une extension de l'algèbre des polynômes en une indéterminée. Il existe plusieurs manières de définir ces polynômes. La plus simple consiste à procéder par récurrence. Une fois la structure A[X₁] construite, on considère l'algèbre A[X₁][X₂] des polynômes en une indéterminée X₂ construite sur l'anneau A[X₁] et on la nomme A[X₁,X₂]. En réitérant n fois, on obtient une algèbre de polynômes en n indéterminées, souvent notée A[X₁,...,X_n].

Une autre méthode consiste à généraliser le mode de construction de A[X]. On considère tout d'abord un ensemble d'indices I, et N^(I) l'ensemble des applications de I dans N à support fini, c'est-à-dire nulle partout, sauf peut-être sur un ensemble fini de points de I. Cet ensemble dispose avec l'addition d'une structure de monoïde. Notons alors A[I], la A-algèbre du monoïde N^(I), c'est-à-dire l'ensemble des applications de N^(I) à valeurs dans A et à supports finis. La structure A[I] est équipée d'une bonne multiplication, qui permet de considérer A[I] comme une A-algèbre. A[I] est en fait A^(N(I)).

Si, dans le cas fini, les deux méthodes sont équivalentes, elles présentent chacune des avantages. La première est plus simple, la deuxième est à la fois plus générale et plus riche. Elle est plus générale car l'ensemble d'indices I n'est pas nécessairement fini ou même dénombrable, ce qui permet de construire des algèbres plus vastes. Elle est aussi plus simple pour établir les propriétés universelles dont dispose l'algèbre. Par exemple, la première construction, dans le cas de l'anneau A[X₁,X₂], donne un rôle différent à X₁ et X₂, pourtant les anneaux A[X₁,X₂] et A[X₂,X₁] sont isomorphes.

Dans la suite de l'article A désigne un anneau commutatif unitaire (et parfois intègre). Seule, cette configuration est étudiée ici. Le terme de A-algèbre désigne une algèbre associative, commutative et unifère.

Deux indéterminées

Construction par récurrence

Considérons l'anneau des polynômes A[X₁][X₂], c'est-à-dire l'anneau des polynômes en une indéterminée X₂, construit sur l'anneau A[X₁], c'est-à-dire l'anneau des polynômes en une indéterminée et à coefficients dans A. L'article Construction des polynômes en une indéterminée, montre que c'est un anneau et un A[X₁]-module de base (X₂ⁿ), si n décrit l'ensemble des entiers positifs N. Un élément P de ce module s'écrit, si n est le degré du polynôme, vu comme un polynôme à une indéterminée à coefficients dans A[X₁]:

Si m est le degré maximal des polynômes P_j(X₁) coefficients de P, il existe une famille d'éléments de A (a_ij) pour i variant de 0 à m et j de 0 à n tel que :

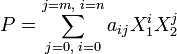
La structure A[X₁] contient, par identification, l'anneau A et l'anneau A[X₁][X₂] dispose naturellement d'une multiplication externe de AxA[X₁], définie par l'égalité suivante, si λ est un élément de A :

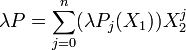
Ce qui s'écrit encore, d'après les propriétés du A-module A[X₁].

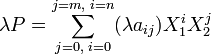
On en déduit, que A[X₁][X₂] dispose d'une structure de A-algèbre associative que l'on appelle A-algèbre des polynômes en deux indéterminées à coefficients dans A et que l'on note A[X₁,X₂] si les deux indéterminées sont symbolisées par les lettres X₁ et X₂.

Construction par un monoïde d'indices

Une autre méthode de construction consiste à calquer le raisonnement utilisé pour les polynômes en une indéterminée, cette fois non pas sur une suite mais sur une famille à double index. Soient S un ensemble à deux éléments et M l'ensemble des fonctions de S dans N, l'ensemble des entiers positifs. On note Y₁^mY₂ⁿ la fonction de M qui vaut m sur le premier élément de S et n sur le deuxième. La structure de monoïde de N confère à M une structure de monoïde, que l'on note multiplicativement :

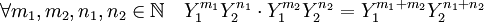
Soit A^(M) l'ensemble des fonctions de M dans A à support fini, c'est-à-dire nulles partout sauf peut-être sur un ensemble fini de points de M. Par construction, l'ensemble A^(M) hérite d'une structure de A-module libre de base Y₁^mY₂ⁿ où n et m décrivent chacun l'ensemble N. Ici . Autrement dit, Y₁^mY₂ⁿ est identifiée à la fonction de M dans A, nulle partout sauf en Y₁^mY₂ⁿ, où elle est égale à 1, l'élément neutre de la multiplication de A. Pour un élément P de A^(M), il existe deux entiers n et m et une unique famille (a_ij) pour i variant de 0 à m et j de 0 à n d'éléments de A tel que :

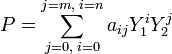
Il existe une bijection Φ entre la structure A[X₁,X₂] construite au paragraphe précédent et A^(M) qui est aussi un morphisme pour l'addition et la multiplication externe. Cette bijection Φ associe X₁^m la fonction Y₁^m, et à X₂ⁿ la fonction Y₂ⁿ, pour tout n et m entiers positifs. La multiplication du monoïde M se prolonge de manière unique en une multiplication sur A^(M). Avec les notations suivantes, si i, j, k, l, r et s sont six indices décrivant N et (b _kl) une famille à support fini de A^(M) :

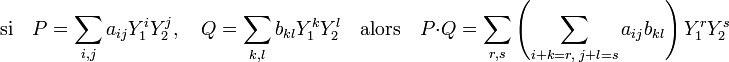
On retrouve la multiplication interne de la structure précédente, le morphisme Φ est un automorphisme de A-algèbre, qui confère à A^(M) muni de sa multiplication, une structure de A-algèbre.

Les deux constructions sont équivalentes et définissent la même structure.

Définitions

Il devient possible de présenter une définition de la structure de A-algèbre des polynômes en deux indéterminées à coefficients dans A.

• Une A-algèbre B disposant de deux éléments canoniques appelées indéterminées et notés ici X₁ et X₂ est qualifiée de A-algèbre des polynômes en deux indéterminées si le monoïde multiplicatif M de base canonique (X₁, X₂) est une base de B considéré comme un A-module. On le note indifféremment A[X₁,X₂], A[M] ou encore A[S] si S est la paire {X₁,X₂}.

Dire que (X₁, X₂) est une base du monoïde revient à dire que tout élément de M s'écrit de manière unique comme produit de puissances de X₁ et de X₂. Ainsi, pour tout élément de M il existe deux entiers positifs n et m tel que l'élément soit égal à X₁^mX₂ⁿ, et si m, n, p et q sont 4 entiers positifs, l'égalité X₁^mX₂ⁿ = X₁^pX₂^q a lieu si, et seulement si les couples (m, n) et (p, q) sont égaux. L'existence d'une A-algèbre des polynômes en deux indéterminées est assurée par les constructions des deux paragraphes précédents.

Certaines définitions données pour le polynôme en une indéterminée se généralisent, un monôme est le produit d'un élément de A par un élément de M, l'élément de A est appelé coefficient. Le degré d'un monôme colinéaire à X₁^mX₂ⁿ désigne l'entier m + n. Le degré d'un polynôme est égal au degré de son monôme de plus haut degré, sauf si le polynôme est nul et on dit que son degré est égal à moins l'infini. La constante d'un polynôme correspond au coefficient du terme X₁⁰X₂⁰, polynôme composé d'un unique terme colinéaire à X₁⁰X₂⁰ est encore appelé polynôme constant. En revanche les termes de polynôme unitaire ou monôme dominant n'ont plus de sens.

Certaines identifications sont immédiates, par exemple l'anneau des polynômes constants s'identifie à A, la sous-algèbre des polynômes de A[X₁,X₂] engendré par X₁ (resp. X₂) est identifiée à A[X₁] (resp. A[X₂]).

On dispose des trois propriétés :

• Il existe une A-algèbre B des polynômes en deux indéterminées.

puis :

• Il existe un unique isomorphisme de A-algèbres de A[X₁,X₂] dans A[Y₁][Y₂] qui à X₁ (resp. X₂) associe Y₁ (resp. Y₂).

enfin :

• Il existe un unique automorphisme de A-algèbres de A[X₁,X₂], qui à X₁ (resp. X₂) associe X₂ (resp. X₁).

Ces trois propriétés sont les conséquences des deux constructions des paragraphes précédents. Ainsi, quelle que soit la manière dont on définit les générateurs de l'ensemble S, la structure finale est la même, à un isomorphisme près.