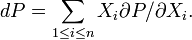Polynôme en plusieurs indéterminées - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Deux indéterminées - Propriétés - Construction de l'algèbre - Polynômes remarquables

Polynômes remarquables

Polynômes homogènes

Un polynôme homogène de degré d (entier positif ou nul) est une combinaison linéaire de monômes de degré d. Le polynôme nul est considéré comme étant de degré d pour tout d. Par exemple, en deux variables, 2X³+X²Y-5Y³ est homogène de degré 3; tandis que 2X³+X²Y³-5Y³ n'est pas homogène. Tout polynôme P de degré (total) d est, de façon unique, somme de polynômes homogènes P_0, ..., P_d de degrés respectifs 0, ...,d. On appelle alors P_i la composante homogène de degré i de P. Dans l'exemple non-homogène ci-dessus, la composante homogène de degré 3 est 2X³-5Y³, celle de degré 5 est X²Y³, les autres composantes homogènes sont nulles. Une autre manière d'exprimer la décomposition en composantes homogènes est de dire que A[X₁, ...,X_n] est la somme directe des A_d[X₁, ...,X_n], où d parcourt les entiers positifs ou nul et où A_d[X₁, ...,X_n] est le sous-A-module des polynômes homogènes de degré d. On note que le produit de deux polynômes homogènes de degrés respectifs d, e est homogène de degré d+e, alors que leur somme n'est homogène que si d=e.

Identité d'Euler: Si P est homogène de degré d, alors

$dP = \sum_{1\le i\le n} X_i \partial P/\partial X_i.$

Polynômes symétriques

Un polynôme à n variables est symétrique s'il est invariant par permutation de deux variables quelconques. Par exemple, en trois variables, X²Y+Y²Z+Z²X est symétrique, alors que X²Y+Y³Z+Z²X ne l'est pas. Contrairement aux polynômes homogènes, les polynômes symétriques sont stables par addition et multiplication, et forment un sous-anneau de l'anneau des polynômes.

Polynômes symétriques élémentaires: pour i entre 1 et n, le i-ième polynôme symétrique élémentaire S_i est la somme des X_k₁...X_{k_i} où les indices parcourent les entiers k₁<...i entre 1 et n. Par exemple, le premier polynôme symétrique élémentaire est la somme des variables, et le dernier est le produit des variables.

Théorème fondamental sur les polynômes symétriques: Tout polynôme symétrique est, de façon unique, une expression polynômiale des polynômes symétriques élémentaires.

Polynômes de Newton: Soit d>0 un entier. Alors P_d:=X₁^d+...+X_n^d est symétrique et est appelé le d-ième polynôme de Newton. L'expression de P_d en fonction des polynômes symétriques élémentaires (comme prédit par le théorème ci-dessus) peut être déduite indirectement par les identités de Newton:

P_d - S₁P_d-1+S₂P_d-2+...+(-1)^n-1S_n-1P_d-n+1+(-1)ⁿS_nP_d-n=0, si d > n - 1 et

P_d - S₁P_d-1+S₂P_d-2+...+(-1)^d-1S_d-1P₁+(-1)^ddS_d=0, si d < n.

Sur un corps de caractéristique nulle, ces relations permettent d'écrire les polynômes symétriques élémentaires comme des polynômes en les polynômes de Newton. En particulier, sur le corps des nombres rationnels, les polynômes de Newton engendrent l'anneau des polynômes symétriques.

Relations entre les zéros et les coefficients d'un polynôme. Soit P(X)=Xⁿ+a₁X^n-1+...+a_n un polynôme de degré n>0 à coefficients dans un corps. Soient t₁,... , t_n les zéros de P(X) (éventuellement répétés) dans un corps de décomposition de P(X). Alors