Polynôme en plusieurs indéterminées - Définition

Construction de l'algèbre

Introduction

L'objectif est de généraliser la construction au cas où l'ensemble S des indéterminées est de cardinal quelconque. L'approche par récurrence s'avère impuissante si le cardinal de S est trop vaste. Si S est fini, elle ne présente aucune difficulté, dans le cas où S est dénombrable, les différentes identifications permettent de considérer l'union d'ensembles emboités :

Cette union s'équipe naturellement de la structure de A-algèbre généralisant la définition du paragraphe précédent. Cette définition est pratique, par exemple pour montrer le caractère factoriel ou noethérien d'une algèbre de polynômes en n indéterminées. Elle est en revanche impraticable pour une configuration où S est de cardinal quelconque. La deuxième méthode est strictement équivalent à la première, si S est dénombrable, mais se prolonge aisément au cas de cardinal quelconque. Elle suppose néanmoins un peu de préparation.

On peut se poser la question de la pertinence d'une démarche qui n'offre, comme unique avantage, que de permettre la construction d'une algèbre de polynômes en un ensemble d'indéterminées non dénombrable. Cette situation n'est en effet pas si fréquente. En revanche, cette construction se fonde sur une démarche permettant une démonstration élégante de propriétés universelles sur les A-algèbres associatives, tel est le principal intérêt de la méthode.

Algèbre de polynômes

Une algèbre de polynômes est un cas particulier d'algèbre d'un monoïde. Soit S un ensemble d'indices et L le monoïde commutatif des fonctions à support fini de S dans N.

• L'algèbre des polynômes à coefficients dans A construite sur S, est l'algèbre du monoïde L. On la note A[S].

On identifie ici l'ensemble S à une partie de A[S] de la manière suivante : A un élément s de S, on associe la fonction e_s de S dans N qui vaut zéro partout sauf en s ou elle vaut 1, l'élément neutre pour la multiplication dans N. Ainsi, e_s est un élément du monoïde L, et plus précisément un membre de la base canonique du monoïde. Ensuite on associe à l'élément e_s, l'élément X_s, correspondant à la famille d'éléments de A indexée par L, qui vaut zéro partout sauf en e_s ou elle vaut 1.

Dans le cas où S est un ensemble fini : {1,...,n}, les éléments de S s'identifient à X_s les éléments canoniques de A[S], on retrouve la notation A[X₁,...,X_n] et le mode construction utilisée bâtir pour A[X₁,X₂]. La propriété universelle du paragraphe précédent prend la forme :

• Soit B une A-algèbre et (b_s) une famille d'éléments de B indexée par S. Il existe un unique morphisme φ de A-algèbre de A[S] dans B tel que :

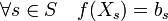
Toutes les A-algèbres ne sont pas des algèbres de polynômes. Considérons le cas où A est égal au corps fini à deux éléments F₂ et M son monoïde multiplicatif (qui est aussi un groupe composée d'un unique élément noté x), la F₂-algèbre du monoïde M, contient 4 éléments {0,1,x,1+x}. On retrouve une F₂-algèbre isomorphe à l'espace des fonctions de F₂ à valeurs dans F₂. Le monoïde M n'est pas un monoïde d'indices car il ne possède pas de base. Une algèbre de polynômes contient toujours une infinité d'éléments car elle correspond à une algèbre de monoïde commutatif ayant une base, et donc une infinité d'éléments.

Notations

Il existe trois manières de noter un polynôme :

• La première correspond aux notations utilisées au paragraphe sur les polynômes en deux indéterminées. Le symbole X_s désigne la famille qui associe 0 à tous les éléments de N^(S) à l'exception de e_s qui est associée à 1, le neutre de l'anneau A. Un monôme s'écrit comme le produit d'un élément de A et d'un monôme spécifique de la forme suivante, où la famille (k_s) est presque nulle et à valeurs dans les entiers positifs :

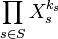
Un polynôme P s'écrit de la manière suivante, utilisée dans les paragraphes précédents et l'algèbre est notée :

• La deuxième manière est plus concise. Elle consiste à noter k la famille (k_s) des coordonnées d'un élément du monoïde dans la base canonique S et X^k le correspondant dans l'algèbre de l'élément du monoïde de coordonnées k dans la base canonique S. Si (a_k) désigne une famille presque nulle de coefficients de A et indexée par N^(S), les notations précédentes deviennent :

• Une troisième approche est utilisée quand l'algèbre des polynômes est construite à partir d'une A-algèbre B et définie à l'aide du formalisme utilisé dans le paragraphe sur les polynômes en deux indéterminées. La lettre S désigne maintenant la base canonique de B. Il est fréquent que les éléments de cette base soient notés à l'aide de minuscules, on trouve la notation K[b₁,...,b_n] dans le cas d'un nombre fini d'indéterminées. Cette notation est aussi utilisée pour décrire n'importe quel image Φ d'un morphisme φ de A-algèbre de K[S] dans B. Ainsi, si b_s désigne l'image de X_s par le morphisme φ, l'algèbre Φ est notée K[(b_s)]. L'ensemble Z[√2, √5] désigne l'image de Z[X₁, X₂] par le morphisme qui à X₁ (resp. X₂) associe √2 (resp. √5). Dans ce cas particulier l'image Φ de n'est pas une Z-algèbre de polynômes car le monoïde sous-jacent n'est pas une base de l'algèbre. Enfin, les algébristes notent aussi A[M] l'ensemble A^(M) muni de la structure de A-algèbre du monoïde M, cette notation est par exemple utilisée dans les articles Algèbre d'un monoïde et Algèbre d'un groupe fini.