Polynôme en plusieurs indéterminées - Définition

Propriétés

Propriétés élémentaires

Certaines identifications ne dépendent pas du caractère fini de S. Ainsi :

• Si S₁ est une partie de S, l'algèbre A[S₁] s'identifie à une partie de A[S].

La proposition, qui permet de construire l'algèbre des polynômes en un nombre fini d'indéterminée, se généralise :

• Si S₁ et S₂ forment une partition de S, l'algèbre A[S] s'identifie à A[S₁][S₂]

La construction par récurrence, illustrée dans le cas des polynômes en deux indéterminées permet de construire un anneau en un nombre dénombrables d'indéterminées. Cette propriété se généralise aussi. Soit S_i, où i est un indice élément d'un ensemble I totalement ordonnée. On suppose la suite croissante pour l'inclusion, c'est-à-dire que si i est plus petit que j, S_i est inclus dans S_j. On note S l'union des S_i.

• L'union des algèbres A[S_i] est égale à A[S].

Enfin :

• Si I est un idéal de A et J l'idéal de A[S] engendré par I, A/I[S] s'identifie à A[S]/J.

Une conséquence de ces propriétés est :

• Si A est un anneau intègre, A[S] l'est aussi.

• Si S₁ est une partie de S, l'algèbre A[S₁] s'identifie à une partie de A[S] :

Il suffit de considérer le morphisme de A-algèbre, qui à s₁, considéré comme un élément de A[S₁] associe s₁, considéré comme un élément de A[S]. C'est un morphisme injectif.

• Si S₁ et S₂ forment une partition de S, l'algèbre A[S] s'identifie à A[S₁][S₂] :

On considère un polynôme P de A[S], il s'écrit de manière unique, avec le deuxième système de notations :

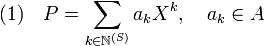
Comme N ^(S) est égal à N ^(S₁) x N ^(S₂), l'égalité précédente s'écrit encore de manière unique :

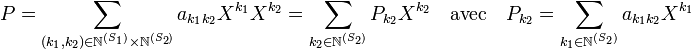
Le morphisme de A[S] dans A[S₁][S₂], qui au polynôme P associe le polynôme de A[S₁][S₂] dont l'écriture est donnée à la ligne précédente est bijectif, ce qui montre la proposition.

• L'union des algèbres A[S_i] est égale à A[S] :

L'identification de A[S_i] à A[S] montre que l'union des A[S_i] est incluse dans A[S]. Réciproquement, un polynôme P s'écrit sous la forme (1) du paragraphe précédent. Chaque monôme est élément des algèbres de l'union, noté ici A[S_k], avec k élément d'un ensemble fini K. Soit h le plus grand indice de l'ensemble K, comme la suite (S_i) est croissante, P est élément de A[S_h] et donc de l'union des algèbres.

• Si I est un idéal de A et J l'idéal de A[S] engendré par I, A / I [S] s'identifie à A[S] / J :

Soit φ l'application de de A dans A / I, qui à a associe sa classe dans A / I. Cette application permet d'en définir une autre de A[S] dans A / I [S] notée Φ et définie par :

Cette application Φ est un morphisme surjectif de A-algèbre, son noyau est J l'idéal de A[S] engendré par I, ce qui démontre la proposition.

• Si A est un anneau intègre, A[S] l'est aussi :

Dans le cadre de cet article, seul les anneaux A intègres sont considérés, ce qui montre que les anneaux de polynômes le sont aussi. Si S est un singleton, il suffit de considérer les deux monômes de plus haut degré pour vérifier que le produit de deux polynômes non nuls est non nul.

Si S est un ensemble fini, il est possible de construire A[X₁, ...,X_n], à l'aide de l'identification A[X₁, ...,X_p-1][X_p], ce qui permet de démontrer la proposition car si A[X₁, ...,X_p-1] est intègre, A[X₁, ...,X_p] l'est aussi.

Si S est un ensemble quelconque et P, Q deux polynômes de A[S], il existe un anneau de polynômes en un nombre fini d'indéterminées contenant P et Q. Si A est intègre, le raisonnement précédent montre que P.Q est non nul.

 

Degré

Dans le cas d'une A-algèbre de polynômes en une indéterminée, l'application degré est un morphisme de monoïde de A[X], considéré comme un monoïde multiplicatif. Cette propriété est toujours vraie. Le degré d'un monôme est la somme des exposants des différentes indéterminées et le degré d'un polynôme est celui de son monôme de plus haut degré. Elle engendre une conséquence importante pour A[X], si les coefficients sont choisis dans un corps commutatif, l'anneau des polynômes est euclidien. Dans le cas d'un anneau de polynômes en plusieurs indéterminée, la proposition devient fausse. Si X et Y désigne deux indéterminées, l'idéal engendré par X et Y n'est pas principal, or un anneau euclidien est toujours principal.

Il est alors nécessaire de rechercher des propriétés plus faibles. Dans le cas d'une unique indéterminée, le morphisme du degré permet d'établir que si A est noethérien, l'anneau des polynômes l'est aussi (cf Anneau noethérien). Le fait que A[X₁,...,X_n][X_n+1] soit isomorphe à l'anneau des polynômes en n + 1 indéterminées, montre par récurrence le résultat suivant, connu sous le nom de Théorème de la base de Hilbert :

• L'anneau des polynômes en un nombre fini d'indéterminées, à coefficients dans A, est noethérien si A l'est.

Ce résultat est faux dans le cas d'un nombre infini d'indéterminées. Si (X_n), où n est un entier strictement positif, désigne une famille infinie d'indéterminées deux à deux distinctes, la suite (J_k) des idéaux engendrés par la famille (X₁, ...,X_k) est strictement croissante et infinie, et l'anneau ne peut être noethérien.

La propriété universelle permet d'en conclure un résultat fondamental en théorie algébrique des nombres. Un anneau d'entiers algébriques d'un corps de nombre est l'image par un morphisme de A-algèbre d'un anneau de polynômes à coefficients dans Z, l'ensemble des nombres entiers, et dont le nombre d'indéterminées est fini. L'image réciproque d'une suite croissante d'idéaux par ce morphisme est une suite croissante dans un anneau noethérien, elle est stationnaire à partir d'un certain rang, en conséquence :

• L'anneau des entiers algébriques d'un corps de nombre est noethérien.

Le morphisme du degré est encore utile si A possède une propriété plus forte. Si un anneau A est factoriel, A[X] l'est encore (cf l'article anneau factoriel). La construction par récurrence de l'anneau des polynômes en un nombre fini d'indéterminées montre que :

• L'anneau des polynômes en plusieurs d'indéterminées, à coefficients dans A, est factoriel si A l'est.

Cette fois-ci, la configuration est un peu différente, le nombre d'indéterminées n'est pas nécessairement fini. Un polynôme est toujours inclus dans un anneau ayant un nombre fini d'indéterminées et l'article Anneau factoriel montre que, dans ce cas là, la décomposition est bien unique. En revanche, le raisonnement précédent ne s'applique plus aux anneaux d'entiers algébriques, ainsi Z[i√3] n'est pas factoriel. En effet, les égalités 4=(1+i√3)(1-i√3)=2x2 correspondent à deux factorisations différentes en facteurs irréductibles d'un élément de Z[i√3].

Propriété universelle

Considérons, pour simplifier, l'anneau des polynômes à n variables A[X₁, ...,X_n]. Soit B une A-algèbre (commutative unitaire). Alors

• Pour tout n-uplet b₁, ..., b_n dans B, il existe un unique homomorphisme de A-algèbres de A[X₁, ...,X_n] dans B qui envoie X_i sur b_i pour tout i entre 1 et n.

Cette propriété, conjuguée au théorème de factorisation, est essentielle pour la construction d'homomorphismes d'une A-algèbre de type fini vers une autre A-algèbre.

Fonction polynomiale

Résultant

Discriminant

Ensemble algébrique

Soit k un corps algébriquement clos. L'ensemble des zéros d'un polynôme f(X₁, ...,X_n) à coefficients dans k est l'ensemble des points (x₁, ...,x_n) dans kⁿ tels que f(x₁, ...,x_n)=0. Un ensemble algébrique dans kⁿ est l'intersection des zéros d'une famille de polynômes dans k[X₁, ...,X_n]. Du fait que l'anneau k[X₁, ...,X_n] est noethérien, il suffit toujours de prendre une famille finie de polynômes. Les ensembles algébriques sont à la base de la géométrie algébrique.