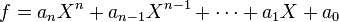Polynôme - Définition

Polynômes formels

Un polynôme f à une indéterminée est défini comme une expression formelle de la forme

où les coefficients a₀,.., a_n sont éléments d'un anneau A, et X est un symbole formel appelé indéterminée du polynôme. Plus formellement, on peut définir un polynôme comme une suite d'éléments, d'un anneau, qui s'annule à partir d'un certain rang. Ainsi, la formule précédente sera une conséquence immédiate (en faisant recours à des notations mathématiques classiques à savoir la notation de Kronecker).Dans ce cas, les coefficients du polynôme coïncident avec les éléments de la suite associée.

L'ensemble des polynômes à une indéterminée X à coefficients dans un anneau A, noté A[X], peut être construit à partir de l'ensemble des suites à support fini (donc nulles à partir d'un certain rang, appelées également suites presque nulles) d'éléments de A, en le munissant d'une structure d'anneau. Dans cette construction un terme aX^k est représenté par la suite qui est nulle partout, sauf que a_k = a.

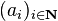
Le degré de ce polynôme est défini, si le polynôme est non nul (c'est-à-dire si ses coefficients ne sont pas tous nuls), par , c'est le plus grand exposant de X devant lequel le coefficient n'est pas nul. On note généralement le degré d'un polynôme P, deg(P) ou . Par convention, le degré du polynôme nul vaut .

Deux polynômes sont égaux si et seulement si les suites de leurs coefficients sont égales. Les polynômes à coefficients dans A peuvent être ajoutés simplement par l'addition des coefficients correspondants, et multipliés en utilisant la distributivité de la multiplication par rapport à l'addition et la règle suivante :

aX ^k bX ^l = ab X ^{k + l} pour tous les entiers naturels k et l.

On peut alors vérifier que l'ensemble de tous les polynômes à coefficients dans l'anneau A forme lui-même un anneau, et que l'application de A vers cet anneau qui envoie a sur a X⁰ est une morphisme injectif d'anneaux. L' « anneau des polynômes à coefficients dans A » est désigné par A[X] et on considère A comme sous-anneau de A[X] par le morphisme mentionné.

Si A est commutatif, alors A[X] est une algèbre sur A.

On peut engendrer l'anneau A[X] à partir de A en adjoignant un nouvel élément X à A et en exigeant que X commute avec tous éléments de l'ensemble A. Pour que l'ensemble obtenu devienne un anneau, toutes les combinaisons linéaires de puissances de X doivent être aussi adjointes à l'ensemble.

Constructions de nouvelles structures

Elles sont de deux types : construction d'extensions sur l'anneau A[X] ou extension sur l'anneau de départ.

Corps des fractions

Si A est un anneau commutatif unitaire intègre, il en est de même de son anneau de polynôme, on peut donc construire son corps des fractions, appelé corps des fractions rationnelles à coefficients dans A et d'indéterminée X.

Corps de rupture

La seconde structure conduit à tout le domaine des extensions.

Si A est un anneau commutatif unitaire intègre et si P est un polynôme premier de A[X], on peut construire un anneau commutatif unitaire intègre contenant A dans lequel P possède une racine.

Si P est un polynôme irréductible (i.e. premier) de K[X], on peut construire un corps commutatif contenant K dans lequel P possède une racine. C'est le corps de rupture de P.

La stratégie de construction nécessite la maîtrise des anneaux et de leurs idéaux. On considère l'idéal I engendré par P . Il est premier si les coefficients sont dans un anneau, il est maximal si les coefficients sont dans un corps. On construit alors l'anneau quotient A[X]/I ou K[X]/I qui se trouve être un anneau commutatif unitaire intègre ou un corps.

On plonge alors A dans cet anneau A_P par le morphisme injectif qui, à l'élément a, associe la classe de a. Et on note r la classe de X. Le calcul de P(r) revient à déterminer la classe de P. Comme P est dans l'idéal I, sa classe est nulle donc P(r) = 0.

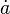
Il est possible de réitérer ce processus jusqu'à obtenir un corps contenant toutes les racines. Ce corps s'appelle le corps de décomposition.

Un corps est algébriquement clos quand il est inutile de chercher des corps de rupture. C’est-à-dire quand tous les polynômes sont scindés. C'est le cas en particulier de .