Polynôme - Définition

Polynôme en plusieurs indéterminées

Le cas de ces polynômes sera juste évoqué ici car l'anneau A[X, Y] peut tout simplement être considéré comme l'anneau des polynômes de la variable Y à coefficients dans A[X].

Le degré du polynôme sera alors la plus grande valeur obtenue en faisant les somme des exposants de chaque indéterminée dans chaque monôme.

est un polynôme de degré 4 à trois indéterminées

Parmi les polynômes à n indéterminées, l'étude des polynômes symétriques et de leur groupe de permutation est un domaine important de l'algèbre.

Ces polynômes sont également dits multivariés, par opposition aux polynômes univariés, à une seule variable.

Autres opérations sur les polynômes

Polynôme dérivé

Sur A[X], si P est le polynôme défini par le polynôme dP défini par si n est non nul et par 0 sinon s'appelle le polynôme dérivé de P.

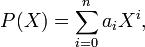
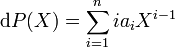
L'application d de A[X] dans A[X] est un morphisme de modules et donc de groupes vérifiant d(PQ) = PdQ + QdP. À ce titre, c'est une application de dérivation, dans un anneau.

Une propriété importante du polynôme dérivé est le fait qu'une racine est multiple si et seulement si elle est aussi racine du polynôme dérivé. En effet, dire qu'une racine r est multiple pour un polynôme P c'est dire qu'il existe n strictement supérieur à 1 et un polynôme Q[X] tel que P[X] = (X − r)ⁿQ[X]. Un simple calcul de dérivé montre alors que dP[X] = n(X − r)^{n − 1}Q[X] + (X − r)ⁿdQ[X].

Division

Si K est un corps commutatif, l'anneau K[X] dispose de deux divisions. La première est euclidienne et confère à l'ensemble des polynômes une structure d'anneau euclidien permettant d'y développer une arithmétique des polynômes un peu analogue à celle des entiers. Cet arithmétique s'avère importante pour la factorisation des polynômes. La deuxième est dite selon les puissances croissantes. Elle est utile dans la recherche d'une décomposition en éléments simples d'une fraction rationnelle ou d'un développement limité.

Polynôme de Laurent

Il est également possible d'introduire les puissances négatives d'une variable et d'obtenir ainsi un anneau A[X,X ^{− 1}] dit de Laurent.