Principe d'équivalence - Définition

Le principe d'équivalence fort

Le principe d'équivalence fort généralise le principe d'Einstein en affirmant que, localement, les effets d'un champ gravitationnel sur toute expérience, même portant sur la gravitation elle même (comme l'expérience de Cavendish par exemple), sont identiques aux effets d'une accélération du référentiel de l'observateur.

Il est équivalent de considérer qu'en tout point de l'espace il existe un référentiel localement inertiel, le référentiel en chute libre dans le champ de gravitation (et en l'absence de tout autre champ extérieur), qu'aucune expérience (gravitationnelle ou non) ne peut distinguer d'un référentiel non soumis à la gravitation.

On ajoute en général l'énoncé, très lié au principe de relativité, que l'expérience est indépendante du lieu et du moment où elle est faite.

Pour ce principe, la notion de local est plus étendue que dans le principe précédent : on peut ainsi considérer que le système solaire dans son ensemble est une expérience gravitationnelle dans un référentiel à peu près inertiel nettement plus grand.

Théories respectant ou pas le principe fort

La relativité générale respecte ce principe du fait que seule la métrique de l'espace-temps détermine le champ de gravitation.

La théorie de Brans-Dicke ne respecte pas ce principe car en plus de la métrique, un champ scalaire détermine la gravitation, et celui-ci ne peut être localement éliminé par un choix de référentiel : même dans un référentiel en chute libre, une expérience gravitationnelle est influencée par ce champ scalaire.

Les théories « à préalable géométrique » couplent la gravitation avec une donnée géométrique non-métrique, locale ou globale (telle qu'une coordonnée temporelle cosmologique, ce que rend possible l'hypothèse du Big Bang) : on conçoit qu'alors le champ de gravitation dépend du lieu ou du moment où il est considéré.

Il n'a pas été démontré rigoureusement que si le principe est respecté alors la gravitation ne dépend que de la métrique de l'espace. La relativité générale semble être la seule théorie métrique respectant le principe fort, mis à part la théorie de Gunnar Nordström datant de 1913, qui respecte la version gravitationnelle du principe fort, mais pas certains aspects du principe d'équivalence d'Einstein, par exemple la déviation de la lumière par la gravité.

Effets du non-respect du principe fort

S'il y a non-respect du principe fort, alors la gravitation a des effets différents dans les différents référentiels qui sont inertiels pour le principe d'Einstein. Même le principe faible serait violé dans les référentiels qui ne seraient pas inertiels par rapport à l'Univers : ainsi le système solaire étant en chute libre dans un champ de gravitation (car seule la gravitation agit dessus), il peut être considéré comme un référentiel inertiel (pour le principe d'Einstein) et les expériences gravitationnelles qui y sont faites dépendent alors du champ de gravitation dans lequel il est plongé, en particulier cela doit pouvoir se détecter sur les expériences testant le principe faible pour des corps massifs (de masse non négligeable par rapport au champ gravitationnel environnant), et dans des mesures précises des mouvements des planètes, voire par une évolution (lente) de la constante gravitationnelle par rapport à l'âge de l'univers.

• L'effet Nordtvedt, prédit par K. Nordtvedt en 1968, dans le cas où le principe fort n'est pas respecté par la théorie métrique utilisée, dit que , où m_p est la masse pesante (ou grave), m est la masse inertielle, E_g > 0 est l'énergie interne du corps (utilisée dans les interactions de ses composants) et μ_N est un coefficient dont l'expression dépend de la théorie métrique. En relativité générale, on a μ_N = 0. Dans les tests du principe faible sur des corps de petite masse, on a , il est donc attendu qu'alors cet effet soit indétectable ; dans le cas d'objets astronomiques tels que le soleil ou la lune, on a , une détection est alors envisageable.

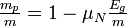
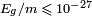
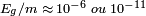
• La dépendance des résultats expérimentaux de tests gravitationnels envers le référentiel en chute libre dans un champ de gravitation se manifesterait par des variations anisotropiques de la constante gravitationnelle dans l'approximation newtonienne et l'on doit alors observer des anomalies dans les mouvements des planètes du système solaire, voire de la lune, des accélérations particulières dans les rotations des pulsars et quelques autres effets inattendus en mécanique newtonienne, effets tellement fins que seules des observations très précises et sur de longues périodes peuvent les détecter.

• La plupart des théories à champ scalaire prédisent une évolution de la constante gravitationnelle G en fonction de l'âge de l'Univers, suivant la formule , où H₀ est la constante de Hubble.

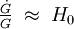
Tests du principe fort

La méthode la plus précise pour tester le principe fort est actuellement le Lunar Laser Ranging (LLR) réalisé par la NASA. L'expérience consiste à utiliser un réflecteur posé sur le sol lunaire (au cours d'Apollo 11 en 1969, suivi par d'autres réflecteurs déposés par Apollo 14 et Apollo 15) pour mesurer la distance terre-lune par des lasers avec une précision d'environ 2 cm (à comparer aux 385.000 km entre la Terre et la Lune), ainsi de petites variations peuvent être détectées. Actuellement, les données permettent de dire que et en année^-1, ce qui conforte l'idée que le principe fort est respecté. De même, les mesures concernant des conséquences de variations spatiales et anisotropiques de la constante gravitationnelle se sont révélées inférieures aux incertitudes de mesures.

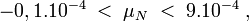
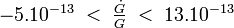
Afin d'affiner les mesures, la NASA envisage la mise en place d'une expérience similaire, mais plus complète, dénommée Apache Point Observatory Lunar Laser-ranging Operation (APOLLO).

Les observations de pulsars binaires n'ont pas donné des mesures plus précises.