Problème de la Belle au bois dormant - Définition

Introduction

Le problème de la Belle au bois dormant est un paradoxe probabiliste polémique, c'est-à-dire pour lequel deux interprétations contraires coexistent sans que l'on soit parvenu à réfuter l'une d'elles. Contrairement au plus célèbre problème de Monty Hall, il n'est pas possible de réaliser une simulation informatique à même de vérifier « expérimentalement » quelle est la bonne solution.

Cet article expose les deux solutions connues, et les principaux arguments en faveur de chacune. Une démonstration plus poussée prétend trancher entre les deux thèses.

Le problème

Le dimanche soir, alors que la Belle au bois dormant (appelons-la Aurore) est endormie, nous lançons une pièce de monnaie pour un tirage à pile ou face. Le tirage n'est pas truqué. Si la pièce tombe sur face, le lendemain (le lundi), on réveille Aurore et on a un entretien avec elle. Si c’est pile, on la réveille le lundi, on a un entretien avec elle, puis on la rendort en lui administrant un somnifère à effet amnésique qui lui fait complètement oublier la journée du lundi. Enfin, toujours dans le cas de pile, on la réveille à nouveau le mardi et on a un autre entretien avec elle.

Au cours de l'entretien, on lui pose la question : « Quelle est la probabilité que la pièce soit tombée sur pile ? »

Étant parfaitement au courant des règles, et maitrisant parfaitement les principes de l'inférence bayésienne, que répondra-t-elle ?

À chaque réveil, Aurore ignore si on est lundi ou mardi. Tout ce qui est dans ce paragraphe est connu de notre princesse.

Afin que le lecteur comprenne bien le sens de la question posée à Aurore, on peut reformuler ainsi le problème : Si, au cours de l'entretien, Aurore dit « La pièce est tombée sur pile », quelle est la probabilité qu'elle ait raison ?

Note : dénomination

Le problème n'a pas grand chose à voir avec le conte de la Belle au bois dormant. Mais le problème a été inventé par des anglophones, et en anglais, le nom du conte est Sleeping beauty (« belle endormie »), ce qui correspond assez bien au problème. C'est par analogie que le nom le plus souvent employé pour ce problème est « Belle au bois dormant ». Ici elle est appelée Aurore par pure commodité.

Bibliographie

• [pdf] Jean-Paul Delahaye, La Belle au bois dormant, la fin du monde et les extraterrestres, Pour la science, n° 309, juillet 2003.
• [pdf] Paul Franceschi, (en) A Two-Sided Ontological Solution to the Sleeping Beauty Problem, Une application des n-univers à l'argument de l'Apocalypse et au paradoxe de Goodman
• [pdf] Laurent Delabre, La Belle au bois dormant : débat autour d'un paradoxe

Ce dernier article constitue la plus récente vue d'ensemble du débat disponible en français. Il propose une bibliographie importante.

Les réponses

Première argumentation « pro-2/3 »

Quand elle se réveille, Aurore distingue trois possibilités :

• On est lundi et la pièce est tombée sur face.
• On est lundi et la pièce est tombée sur pile.
• On est mardi et la pièce est tombée sur pile.

Cela fait donc 2 chances sur 3 pour que la pièce soit tombée sur pile. Mais l'hypothèse d'équiprobabilité est très arbitraire, il faudra la justifier plus rigoureusement.

Première argumentation « pro-1/2 »

La pièce n'étant pas truquée, il y a une chance sur deux pour qu'elle soit tombée sur pile, une chance sur deux pour qu'elle soit tombée sur face. Dans le cas de pile, il y a deux entretiens successifs, un premier le lundi, l'autre le mardi. Ce sont des sous-cas équiprobables du cas où la pièce tombe sur pile. Les probabilités sont donc :

• On est lundi et la pièce est tombée sur face : 1/2
• On est lundi et la pièce est tombée sur pile : (1/2)×(1/2)=1/4
• On est mardi et la pièce est tombée sur pile : (1/2)×(1/2)=1/4

La probabilité pour que la pièce soit tombée sur pile n'est donc pas de deux tiers mais d'un demi. Mais les probabilités semblent ici avoir été attribuées tout aussi arbitrairement. Surtout, y a-t-il vraiment eu un tirage au sort entre lundi et mardi après que la pièce est tombée sur pile?

Argumentation plus poussée « pro-2/3 »

L'ébauche d'argumentation posait froidement l'équiprobabilité des trois hypothèses pour Aurore. Est-ce légitime ? Regardons de plus près : quand Aurore se réveille, elle sait qu'on est ou bien lundi ou bien mardi.

• Si on lui dit qu'on est lundi, le problème se résume à : « La pièce est-elle tombée sur pile ou sur face dimanche ? ». Les probabilités sont alors de 1/2 pour pile, 1/2 pour face.
• Or, il y a également la possibilité pour qu'on soit mardi, qui impose que la pièce soit tombée sur pile.

Ainsi, la probabilité pour que la pièce soit tombée sur pile quand on ignore le jour est quelque part entre 1/2 et 1, et est donc supérieure à la probabilité que la pièce soit tombée sur face.

Plus précisément :

Quelle est la probabilité pour qu'on soit mardi ? Il y a un entretien le lundi quel que soit le côté sur lequel est tombé la pièce, et le mardi seulement en cas de pile. Il est donc deux fois plus probable qu'on soit le lundi. Cela donne comme possibilités :

• On est lundi et la pièce est tombée sur face : (2/3)×(1/2)=1/3
• On est lundi et la pièce est tombée sur pile: (2/3)×(1/2)=1/3
• On est mardi et (donc) la pièce est tombée sur pile : 1/3

On voit ici qu'il était raisonnable de postuler l'équiprobabilité des 3 cas d'entretiens, dans la première argumentation : on a autant de chance de se trouver dans chacune des 3 situations. On peut remarquer que dans des variantes où on relance la pièce plusieurs fois, cela ne serait plus vrai.

D'un point de vue statistique :

Sur 100 expériences, le pièce tombera 50 fois sur pile, avec 2 entretiens à chaque fois, et 50 fois sur face, avec 1 entretien à chaque fois. Soit en tout 150 entretiens dont 100 au cours desquels la bonne réponse est pile.

Finalement, Aurore semble avoir intérêt à répondre pile.

Défauts de l'argumentation « pro-1/2 »

Dans l'argumentation « pro-1/2 », on a supposé que « lundi » et « mardi » sont des sous-cas équiprobables de : « La pièce est tombée sur pile ». Est-ce bien raisonnable ? On pourrait en fait distinguer quatre cas :

• On est lundi et la pièce est tombée sur face.
• On est lundi et la pièce est tombée sur pile.
• On est mardi et la pièce est tombée sur pile.
• On est mardi et la pièce est tombée sur face.

Et il peut sembler légitime de les considérer comme équiprobables.

Aurore sait à son réveil qu'elle est dans un de ces quatre cas, et une fois qu'elle reconnait que le lit où elle se trouve est celui du laboratoire, elle peut exclure le quatrième cas. On applique alors la formule de Bayes pour trouver la probabilité des hypothèses restantes :

• On est lundi et la pièce est tombée sur face :
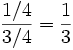
• On est lundi et la pièce est tombée sur pile :
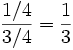
• On est mardi et (donc) la pièce est tombée sur pile :

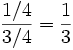
On retrouve le résultat annoncé. Mais la considération « les quatre situations initiales sont équiprobables » apparaît arbitraire, et on peut également se demander si la nouvelle information laisse invariante les autres probabilités, autorisant une application directe de la formule de Bayes.

Et sans le mardi ?

Que se passe-t-il si on révèle à Aurore qu'on est le lundi ? En admettant l'hypothèse « 2/3-1/3 », la formule de Bayes ramène les probabilités à 1/2 pour pile, 1/2 pour face. En revanche en admettant « 1/2-1/2 » dans le cas principal, il y a cette fois 2 chances sur 3 pour qu'Aurore doive répondre « face » ! S'il semble difficile à certains d'accepter que le cas "avec le mardi" conduise à 2/3-1/3, prétendre que le cas des 3 entretiens est régit par la loi 1/2-1/2 conduit à 2/3-1/3 dans une situation qui semble pourtant équivalente à un problème parfaitement symétrique entre pile et face.

Dans tous les cas, on est bien obligé d'admettre que parfois la pièce a 2 chances sur 3 d'être tombée sur un côté (sauf à refuser la formule de Bayes, mais ce n'est pas une argumentation acceptable). Ceci étant dit, l'affirmation initiale des 2/3-1/3 pour le cas des trois entretiens peut maintenant sembler plus vraisemblable.

De plus, on trouve alors que si on informe Aurore qu'on est le lundi, savoir si un entretien peut avoir lieu ou non le mardi n'a plus d'influence sur la probabilité aux yeux des partisans du 2/3-1/3, alors que les partisans du 1/2-1/2 obtiennent le résultat assez contre-intuitif que l'existence du réveil du mardi a une influence sur la réponse du lundi même quand on sait qu'on est le lundi.

Explication par l’effet de loupe

Une explication « intuitive » du résultat « 2/3-1/3 » serait « il y a deux fois plus d’entretiens quand la pièce est tombée sur pile donc quand il y a un entretien, il y a deux fois plus de chances pour que la pièce soit tombée sur pile ». C’est précisément ce qu’on appelle effet de loupe en probabilité.

Un cas d’effet de loupe plus facile à saisir est celui du pêcheur : sachant que la moitié des poissons du lac font moins de cinq centimètres, son filet va capturer pour moitié des poissons de moins de cinq centimètres. Mais la moitié s’échappera du filet contre aucune fuite concernant les gros. En prenant un poisson au hasard dans le filet, on a donc 2 chances sur 3 que ce soit un gros puisqu’il y a 2/3 de gros parmi les poissons remontés.

Le cas du pêcheur est beaucoup plus simple mais c’est justement pour ça qu’il n’est pas évident que la situation de la Belle au bois dormant soit analogue.

En fait il n'y a aucun paradoxe, il faut simplement distinguer le phénomène aléatoire (lancer de pièce : probabilité 1/2 pour pile ou face) de son observation : probabilité pour la princesse d'observer pile (deux fois plus d'entretiens que si c'est face donc probabilité 2/3).

On peut imaginer un jeu qui reproduise ce phénomène. Vous construisez une caisse fermée avec deux compartiments numérotés A et B, dans un de ces compartiments vous enfermez une boule. Vous mettez deux caméras dans le compartiment où se trouve la boule et une dans le compartiment vide. Ces caméras sont numérotées aléatoirement de 1 à 3 et reliées à un écran. Vous demandez à un joueur de choisir un numéro de caméra et d'appuyer sur le bouton portant ce numéro, cela donnera l'image captée par la caméra sur l'écran. Il a 2 chances sur trois de voir la boule et pourtant si vous lui demandez de choisir un compartiment de la caisse A ou B il n'a qu'une chance sur deux de trouver la boule.

Le cas des urnes

Une autre expérience est proposée pour faciliter le raisonnement: on se trouve face à deux urnes: l'urne 1 contient une émeraude, l'urne 2 une émeraude et un rubis (on ne peut les distinguer au toucher). On tire à pile ou face: si la pièce tombe côté face, on tire un joyau dans l'urne 1. Si la pièce tombe sur pile, dans l'urne 2. En construisant un arbre (tous les tirages sont équiprobables) on trouve rapidement que la probabilité de tirer le rubis est d'un quart. Mais on pourrait proposer une argumentation "statistique" menant à une autre réponse: si on répète l'expérience 100 fois, on aura finalement choisi 100 joyaux au hasard parmi 100 émeraudes et 50 rubis (on pioche une fois sur deux dans l'urne 2). D'où on déduit une chance sur 3 de tirer un rubis.

Peut-on trancher? En effet, il apparaît comme incorrect d'avoir mélangé les émeraudes de l'urne 1, dont le tirage est infaillible, avec les joyaux de l'urne 2, dont le tirage n'a lieu qu'une fois sur 2. On a ainsi assigné la même probabilité à un tirage d'émeraude dans l'urne 1 et dans l'urne 2, contredisant notre arbre initial.

Certains partisans du 1/2 pensent que les partisans du 2/3 font la même erreur dans le problème de la Belle au bois dormant. Mais l'équivalence des problèmes n'est pas évidente: puisque les deux réveils "pile-lundi" et "pile-mardi" ont lieu, le cas d'Aurore ne ressemble-t-il pas à une expérience de l'urne où on tirerait les deux joyaux de l'urne 2? On aurait ensuite à déterminer la probabilité du pile et du face à partir d'un seul joyau, et la manière de choisir un joyau parmi les 1 ou 2 de manière à rendre le problème équivalent à celui d'Aurore n'est pas clairement établi.

Passage au cas limite

Il est raisonnable que chaque côté d'une pièce de monnaie puisse se voir attribuer une probabilité autre que 1/2. Passons à un cas plus extrême : on lance la pièce le dimanche, et si elle tombe sur face, on poignarde Aurore dans son sommeil. Si elle tombe sur pile, on la réveille le lundi matin. Aurore connaissant les règles, on lui demande quelle est la probabilité que la pièce soit tombée sur face. Elle répondra zéro, puisqu'elle se sait vivante.