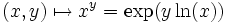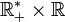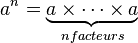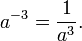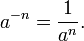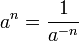Puissance (algèbre) - Définition

Introduction

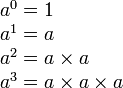
En algèbre, l'opération puissance consiste à multiplier un nombre a par lui-même plusieurs fois de suite. Le nombre de facteurs intervenant dans cette opération est noté à la suite du nombre a en exposant au sens typographique de ce terme. Pour cette raison, ce nombre de facteurs est encore appelé exposant (sens mathématique) de l'opération puissance, et ce nom remplace parfois abusivement le nom de l'opération elle-même.

Ainsi, si n est un entier naturel supérieur ou égal à deux et a un nombre réel ou complexe :

qui est lu « a puissance n » ou abusivement « a exposant n ». En particulier, le carré et le cube sont des puissances d'exposant 2 et 3 respectivement. Tout élément est égal à sa propre puissance d'exposant 1, tandis que toute puissance d'exposant nul vaut 1 par convention.

Lorsqu'un élément est inversible, ses puissances d'exposant négatif sont définies comme les puissances de son inverse. Par exemple, si a est un nombre réel non nul :

L'opération puissance est prioritaire sur les autres opérations algébriques élémentaires.

Les opérations algébriques sur les puissances d'un nombre ou de plusieurs possèdent des propriétés particulières. Les puissances de 10, comme 10⁻⁵, sont d'une utilisation régulière dans les autres sciences, notamment en physique et en chimie.

Puissance à exposant positif

On considère un nombre a quelconque et un entier naturel n non nul. La puissance énième de a, notée aⁿ et lue «  a puissance n », ou « a exposant n » est le résultat de la multiplication de ce nombre a par lui-même n fois :

Le nombre n est appelé l'exposant de la puissance aⁿ.

Le nombre n est un entier naturel (donc positif) et aⁿ est une puissance à exposant entier positif de a.

Cas particuliers

• a¹ = a ;
• On appelle a² la puissance carrée ou le carré de a ;
• On appelle a³ la puissance cubique ou le cube de a.

On remarque facilement que, quel que soit l'entier naturel n non nul, 0ⁿ = 0 ainsi que 1ⁿ = 1.

Puissance à exposant négatif

On considère maintenant un nombre a non nul et un entier naturel n. Le nombre a^-n, lu « a puissance moins n », ou « a exposant moins n » par abus de langage, est l'inverse de la puissance énième de a, c'est-à-dire :

On comprend qu'il ait fallu exclure 0 de cette définition car l'inclure serait revenu à vouloir diviser par 0, ce qui est impossible.

Le nombre -n est l'exposant de la puissance a^-n.

Le nombre -n étant négatif, car n est un entier naturel, a^-n est une puissance de a à exposant négatif. On notera, en particulier, que a⁻¹ = 1/a (l'inverse du nombre a ).

On peut appliquer cette règle pour transformer une puissance positive en inverse d'une puissance négative :

Puissance à exposant zéro

Pour tout nombre réel a strictement positif, on pose par convention que a⁰ = 1. En effet, on peut écrire d'où a⁰ = 1.

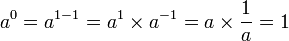
Dans certains contextes, il peut être utile de poser la convention 0⁰ = 1, par exemple pour identifier le polynôme X⁰ avec la fonction constante de valeur 1. De même, dans le cadre de la théorie des ensembles, la notation 0⁰ peut représenter le nombre d'éléments de l'ensemble des applications de l'ensemble vide dans lui-même et donc valoir 1.

Cependant, l'application , bien définie sur n'admet pas de prolongement par continuité en (0,0) ce qui interdit le choix d'une convention acceptable en toute généralité.