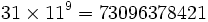Pyramide de 11 - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La Pyramide de 11 est une variante du triangle de Pascal. Elle permet de calculer exactement les puissances de 11 ou
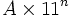
Règles
La pyramide de 11 permet de calculer par additions sucessives, sans multiplication, le produit d'un nombre naturel par une puissance de 11. Elle s'obtient en additionnant par paire successivement de droite à gauche, par saut de un chiffre, les chiffres successifs qui composent ce nombre entier naturel multipliant une puissance de 11, la première ligne étant celle du nombre en question, la ligne suivante le nombre obtenu par ce calcul par paires, et ainsi de suite pour les lignes suivantes. La première ligne correspond en fait au nombre multipliant 11 puissance 0, la deuxième au nombre multipliant 11 puissance 1, et ainsi de suite, la (n+1)ième ligne étant le résultat du nombre de départ multipliant 11 puissance n. Prenons par exemple le nombre 2156478 comme multiplicateur d'une puissance de 11, et calculons le nombre qui apparaîtra sur la ligne suivante, qui sera le résultat du produit de ce nombre par 11. Pour l'application de la règle, ce nombre de départ s'écrira 02156478,0, par rajoute d'un zéro "virtuel" de chaque côté du nombre. Les additions par paires successives de gauche à droite seront les suivantes : "8+0" (car le nombre 2156478 = 2156478,0), "7+8", "4+7", "6+4", "6+5", "5+1", "2+1" et "0+2" (pour terminer le nombre obtenu car 2156478 = 02156478). Si le résultat de ces additions est supérieur ou égal à 10 alors on prend le dernier chiffre composant le résultat et on retient 1 qui sera rajouté à la paire suivante à gauche. Les résultats possibles à toutes ces additions appartiennent à cet intervalle :
Un résultat nul est en effet possible, si le nombre comporte plusieurs 0 consécutifs, par exemple 2006. Reprenons l'exemple du début, le résultat de 2156478 par la multiplication de 11 (en fait 11 exposant 1) est :
Détaillons plutôt le calcul :
- 8+0=8, on pose le 8 en premier
- 8+7=15, on pose le 5 avant le 8 et on retient 1 pour l'addition suivante
- 7+4+1=12, on pose le 2 avant le 5 et on retient 1 pour l'addition suivante
- 6+4+1=11, on pose le 1 avant le 2 et on retient 1 pour l'addition suivante
- 6+5+1=12, on pose le 2 avant le 1 et on retient 1 pour l'addition suivante
- 5+1+1=7, on pose le 7 avant 2
- 2+1=3, on pose le 3 avant le 7
- 2+0=2, on pose le 2 avant le 3.
Ceci est la dernière opération car on est arrivé au premier chiffre qui compose le nombre à calculer. On effectue la même opération sur ce chiffre 23721258 obtenu pour calculer
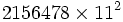
La puissance "n" (
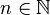
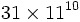
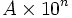

Cette formule ne fonctionne pas quand le nombre de lignes dépasse 10.
Exemples
Avec 1 comme nombre de départ
Ici : 117 = 19487171
En reprenant l'exemple cité dans la règle de calcul utilisée dans la pyramide, calculons
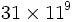
Donc :