Pyramide de 11 - Définition

Démonstration

On peut essayer avec n'importe quel chiffre, la technique de la pyramide de 11 fonctionne tout le temps. Comment alors peut-on démontrer qu'une telle méthode peut marcher ?

Essayons de calculer cette opération :

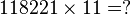
Posons la multiplication comme suivant :

       118221      x    11      -------      =118221      1182210      -------      1300431      

On remarque que multiplier par 11 un nombre c'est de faire la somme entre deux de ces chiffres voisins. Il est donc plus facile sans poser la multiplication de passer directement à la méthode de la pyramide de 11

118221 1300431

Généralisation

La pyramide de 11 fonctionne en base 10. On peut faire de même dans une base n, pour le nombre n+1. Néanmoins il ne faut pas oublier de convertir les nombres en base 10 et de respecter le maximum du nombre de ligne qui est n.

Exemples

Pour 5^n en base 4:

5^n	pyramide de 11	pyramide de 5
50	1	1
51	11	5
52	121	25
53	1331	125

Réciproque

La réciproque de la Pyramide de 11 est plus intéressante mais est beaucoup plus dure à appliquer.

Exemples

Cas d'un nombre divisible par 11

Montrer que 1816474 est un multiple de 11

On envisage de poser 1816474 et on recherche les soustractions possibles à ce nombre.

1816474,0

La première soustraction (en partant de la droite) est évidente car c'est 4-0=4.

1816474 xxxxx4
(x representant un chiffre)

Pour 7, il fallait au préalable que le deuxième chiffre du précédent nombre soit un 3 car 7-4=3 On ne peut pas avoir 14 car ce nombre est composé de 2 chiffres

1816474 xxxx34

Ensuite, par déduction, le troisième chiffre du précédent nombre est 1 car 4-3=1

1816474 xxx134

Ainsi de suite :

• 6-1=5
• 11-5=6 (on ne peut pas faire 1-5 car sinon le résultat appartiendrait à )
• 8-6=2-1=1

On obtient donc

1816474 165134

On peut en déduire que :

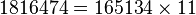
Cas d’un nombre non divisible par 11

Montrer que 18225 n’est pas divisible par 11

Pour montrer que 18225 n’est pas divisible par 11, il faut montrer que la réciproque de la pyramide de 11 ne marche pas. C’est-à-dire qu’une addition du résultat de la réciproque ne fonctionne pas pour donner le dernier chiffre.

18225 xxx5

Premièrement, pour avoir le premier chiffre du résultat de la réciproque, il faut tout simplement faire 5-0=5. Ensuite, le deuxième chiffre s’obtient en faisant 12-5 (et non 2-5 car le résultat est un chiffre négatif). On obtient 7 et on retient 1.

18225 xx75

Les soustractions suivantes sont :

• 12 − 1 − 7 = 4
• 8 − 1 − 4 = 3

Le résultat de la réciproque serait 3475 mais donc la réciproque ne fonctionne pas et donc on peut en déduire que 18225 n’est pas divisible par 11.

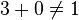
Organisation par un tableau

C'est une autre méthode pour trouver les chiffres qui composent le résultat de la réciproque. Par exemple, prenons le nombre 37250615421. On veut savoir s'il est divisible par 11. On appelle R_n les chiffres qui composent le premier nombre et T_n le résultat de la réciproque.

37250615421 xxxxxxxxxx

On organise le résultat de la réciproque par un tableau regroupant les opérations à faire :

	R	T1	Ret.	T2
1	1	0	0	1
2	2	1	0	1
3	4	1	0	3
4	5	3	0	2
5	11	2	0	9
6	16	9	1	6
7	10	6	1	3
8	5	3	1	1
9	2	1	0	1
10	7	1	0	6
11	6	0	0	6

Comme , le nombre n’est pas divisible par 11

Explication du fonctionnement du tableau et des retenues

Tout d'abord, on compte le nombre de chiffres qu'il y a dans le nombre où on cherche la divisibilté par 11. Il y aura autant de lignes dans le tableau que de chiffres. Dans la ligne d'en tête, on retrouve quatre colonnes : R (le chiffre du nombre de la première ligne), T₁, le premier chiffre en partant de la droite ; Ret. où on met les retenues et T₂, le deuxième chiffre en partant de la droite calculé.

Pour trouver T₂, il faut faire la soustraction R − T₂. À la première ligne, T₁ est toujours égal à 0. On peut aussi remarquer que T₂ de la première ligne est toujours égal à T₁. En numérotant les lignes, on s'y retrouve plus facilement. R est déterminé par le nième chiffre qu'on veut calculer.

Si R est inférieur à T₁, il faut ajouter 10 à R mais à la ligne suivante, il faudra retrancher un 1 au résultat final.

Généralisation

Soit deux nombres qui s’écrivent :

ou ou

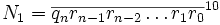
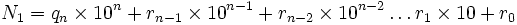
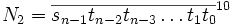
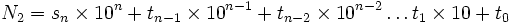
On veut montrer la divisibilité par 11 de ce nombre en appliquant la réciproque de la pyramide de 11. Pour cela, il faut montrer qu’un deuxième nombre (N₂) existe tel que :

• t₀ = r₀ − 0
• t₁ = r₁ − t₀
• t₂ = r₂ − t₁

ou plus généralement r_n = r_{n − 1} − t_{n − 1}.

On a la construction suivante :

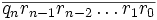
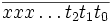
Si , on peut ajouter 10 à r_{n − 1}. Mais pour faire cela, il faut avoir cette soustraction r_{n + 1} = r_n − 1 − t_n