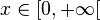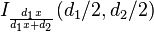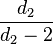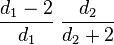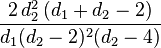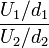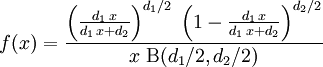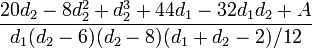Loi de Fisher - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Fisher-Snedecor | |
|---|---|
| |
| |
| | |
| Paramètres |  degré de liberté degré de liberté |
| Support |
|
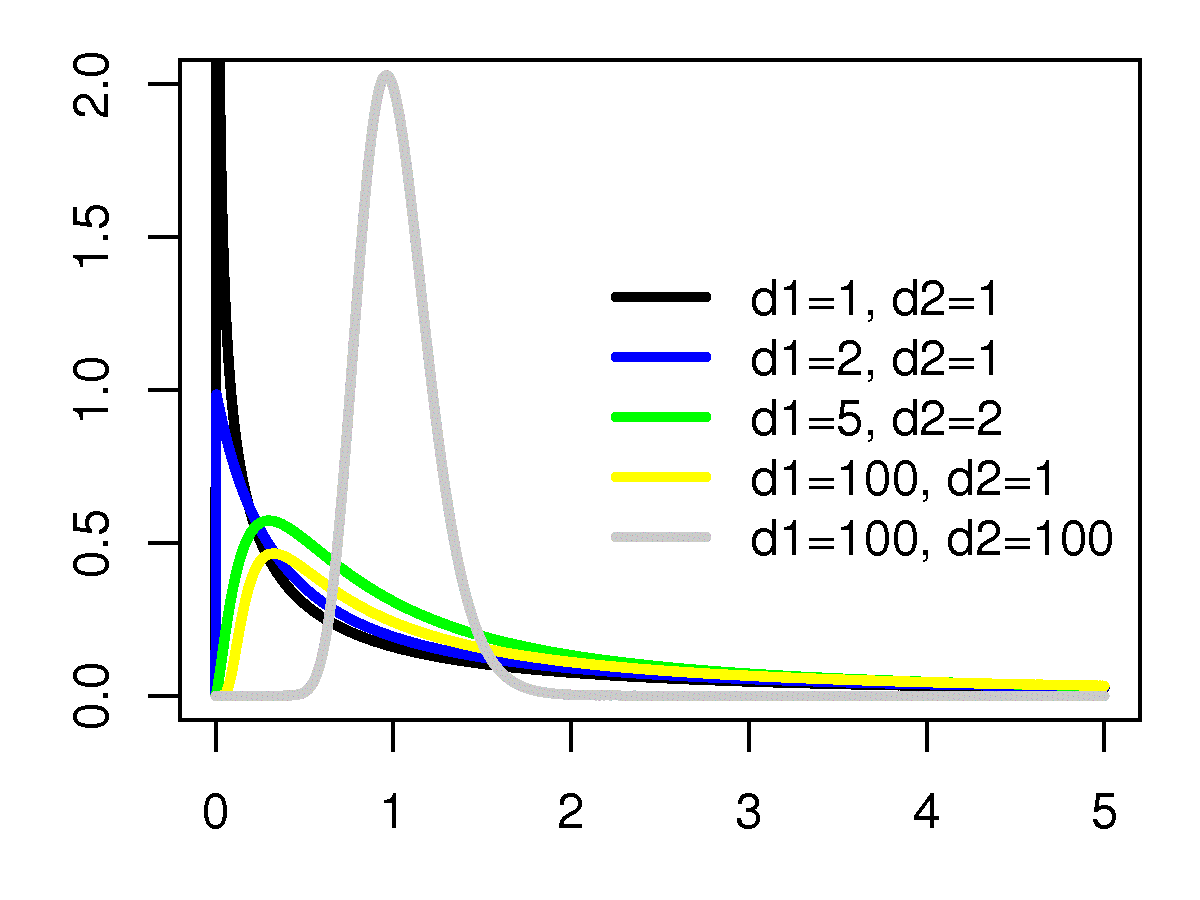
| Densité de probabilité (fonction de masse) |
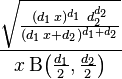
|
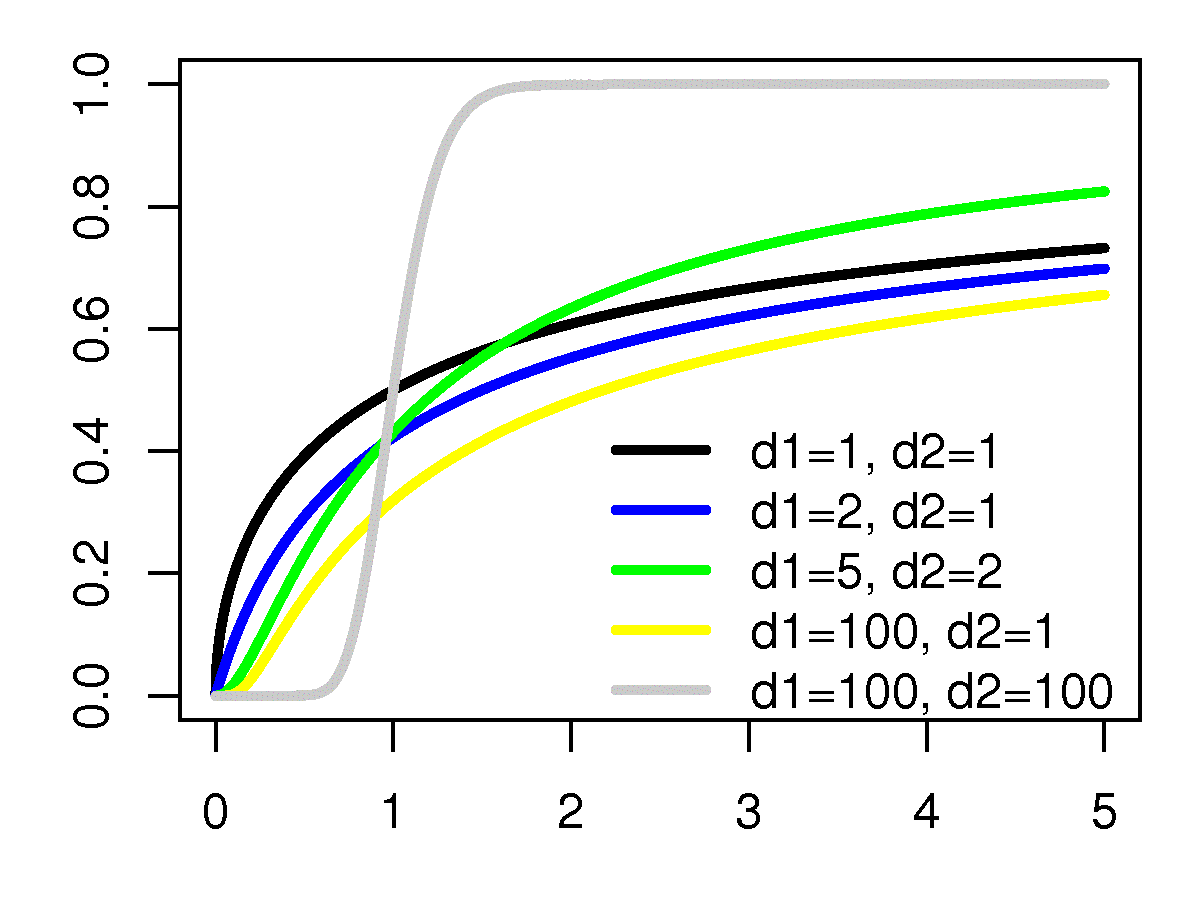
| Fonction de répartition |
|
| Espérance |
|
| Mode |
|
| Variance |
|
| Asymétrie (statistique) |
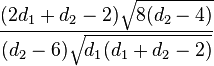
pour d2 > 6 |
| Kurtosis (non-normalisé) | voir texte |
| modifier | |
Dans la Théorie des probabilités et en Statistiques, la loi de Fisher ou encore loi de Fisher-Snedecor ou encore loi F de Snedecor est une loi de probabilité continue. Elle tire son nom des statisticiens Ronald Aylmer Fisher et George W. Snedecor. La loi de Fisher survient très fréquemment en tant que distribution de l'hypothèse nulle dans des tests statistiques, comme par exemple les tests du ratio de vraisemblance ou encore dans l'analyse de la variance (F-test).
Caractérisation
Une variable aléatoire réelle distribuée selon la loi de Fisher peut être définie comme le quotient de deux variables aléatoires indépendantes, distribuées selon une loi du χ²:
avec U1 et U2 ayant respectivement d1 et d2 degrés de liberté.
La densité de probabilité d'une loi de Fisher, F(d1, d2), est donnée par
pour tout réel x ≥ 0, où d1 et d2 sont des entiers positifs et B est la fonction bêta.
La fonction de répartition associée est
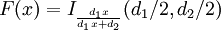
où I est la fonction bêta incomplète régularisée.
L'espérance, la variance valent respectivement
pour d2 > 2 et
pour d2 > 4. Pour d2 > 8, le kurtosis est
où
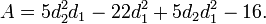
Distributions associées et propriétés
- Si
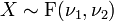
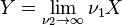
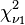
- La loi F(ν1,ν2) est équivalente à la loi T-square de Hotelling's
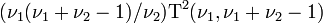
- Si
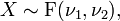
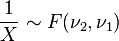
- Si
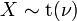
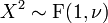
- Si
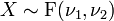
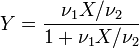
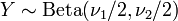
- Si

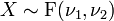
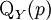
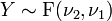
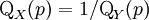
Généralisation
Une généralisation de la loi de Fisher est la loi de Fisher non centrée.