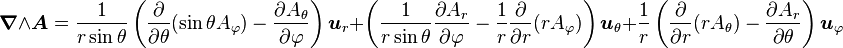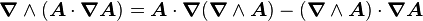Rotationnel - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Unité
Dans le cas usuel où les coordonnées de la base représentent des longueurs, l'unité du rotationnel est alors l'unité du champ considéré divisée par une unité de longueur. Par exemple, l'unité du rotationnel d'un champ de vitesse est le radian par unité de temps, comme une vitesse angulaire.
Règles de calcul
Linéarité
Pour toute constante c réelle et pour tous champs vectoriels A et B
-
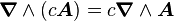
-
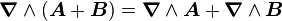
Composition avec une autre quantité
-

-

Composition avec plusieurs opérateurs
-
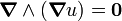
-
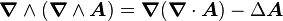
(Voir rotationnel du rotationnel)
Expression dans d'autres systèmes de coordonnées
En coordonnées cylindriques
-
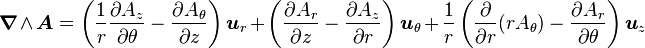
En coordonnées sphériques
-