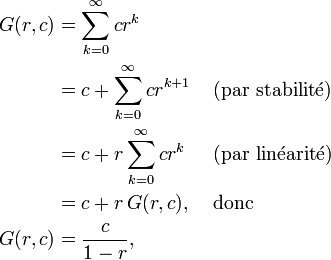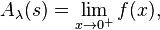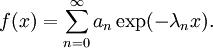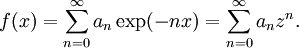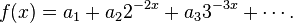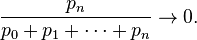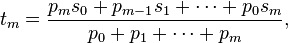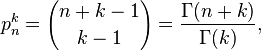Série divergente - Définition

Point de vue axiomatique

Le point de vue axiomatique consiste à trouver des conséquences sur les propriétés d'une méthode de sommation à partir des propriétés de base. Par exemple, toute méthode régulière, stable et linéaire qui parvient à sommer les séries géométriques de raison différente de 1 les somme à la même valeur, spécifiée dans le calcul suivant :

Les méthodes de sommation d'Abel

Soit λ = {λ₀, λ₁, λ₂, …} une suite de réels positifs strictement croissante tendant vers l'infini. La somme d'Abel liée à la suite λ d'une série s de terme général a_n est

sous la condition que la somme suivante définissant la fonction f soit convergente pour x assez proche de 0 :

Les séries de cette forme sont des généralisations des séries de Dirichlet.

Ces méthodes de sommation sont régulières, linéaires, stables, mais il n'y a pas en général consistance entre deux telles méthodes (i.e pour deux choix distincts de λ).

Sommation d'Abel

Dans le cas λ_n = n, on obtient par le changement de variables z = exp(-x) l'expression :

Et la limite de f quand x tend vers 0 est donc la limite de la série entière ci-dessus quand z tend vers 1 (le long de l'axe réel, par valeur inférieure).

Cette sommation particulière est compatible avec et plus forte que la sommation de Cesàro à n'importe quel ordre.

Sommation de Lindelöf

Dans le cas λ_n = n ln(n), on obtient :

La limite quand x tend vers 0 est la somme de Lindelöf de la série de terme général a_n. Cette méthode a des applications aux séries entières.

Moyennes de Nörlund

Soit p=(p_n)une suite à termes positifs et vérifiant la convergence :

Soit une suite s, de terme général s_m. Sa moyenne de Nörlund relativement à la suite p est la limite de la suite de terme général :

et elle est notée N_p(s).

Ces méthodes de sommations sont régulières, linéaires, stables, et consistantes entre elles. Pour k entier strictement positif, le cas particulier de la suite p^k de terme général :

est la méthode de sommation de Cesàro d'ordre k, notée C_k, avec donc : C_k(s) = N_(p^k)(s). Il est usuel de considérer que C₀ est la sommation des séries convergentes, et que C₁ est la sommation de Cesàro ordinaire. Pour h > k, la sommation de Cesàro d'ordre h est plus forte que celle d'ordre k.

Bibliographie

Vulgarisation

• Jean-Pierre Ramis ; Les séries divergentes, Pour La Science 350 (Décembre 2006), 132-139.

Bibliothèque virtuelle

• Journées X-UPS ; Séries divergentes et procédés de resommation, (1991). pdf. Contient les quatre contributions suivantes :
  • Jean-Pierre Ramis ; Séries divergentes et théories asymptotiques ;
  • Michèle Loday-Richaud ; Séries formelles provenant de systèmes différentiels linéaires méromorphes ;
  • Jean Thomann ; Procédés formels et numériques de sommation de séries solutions d'équations différentielles ;
  • Alain Chenciner ; Séries divergentes de la mécanique céleste (problèmes planétaires).

Ouvrages de référence

• Émile Borel ; Leçons sur les séries divergentes, Gauthier-Villars, Paris (Deuxième édition - 1928).
• Godfrey H Hardy ; Divergent Series, Oxford University Press (1949). Réédition : American Mathematical Society (1992), ISBN 0-8218-2649-2.
• Jean-Pierre Ramis ; Séries divergentes et théories asymptotiques, Panoramas et Synthèses 0 (1994), ISBN 2-85629-024-8.
• Bernard Malgrange ; Sommation des séries divergentes, Expositiones Mathematicae 13 (1995), 163-222.
• Leonhard Euler Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques, Mémoires de l'academie des sciences de Berlin 17, 1768, pp. 83-106; Opera Omnia: Series 1, Volume 15, pp. 70 - 90; Euler Archive: E352.