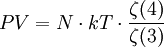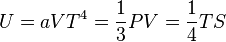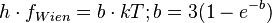Système d'unités du corps noir - Définition

Thermodynamique du corps noir

Le nombre de photons par unité de volume est d.u.[kT, , c] = .

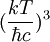
Pour le calcul exact, multiplier par

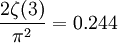
Ainsi la loi du gaz de photons est remarquable de simplicité :

Équation d'état exacte du gaz de photons

(pour mémoire, on rappelle que la fonction Zêta(s) de Riemann vaut 1.2020... pour s = 3 et pour s = 4).

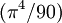
• Si l'on dilate lentement et réversiblement le volume d'un corps noir, chaque longueur d'onde subit l'effet Doppler, sans qu'il y ait variation du nombre de photons dans chaque mode propre : c'est dire que l'entropie S varie comme V.(kT)^3 :

très exactement G = H-TS = 0 pour un corps noir.

Thermodynamique du corps noir

Application au fond diffus cosmologique

Penzias et Wilson ont reçu le prix Nobel en 1978 pour avoir détecté ce rayonnement prévu par Gamow. Lors du Big Bang, l'univers s'est dilaté et la température a baissé et la formation d'atomes (H+) + (e-) -> H a pu se produire. Il s'est produit alors découplage entre matière neutre et rayonnement.

Depuis, le nombre de photons "fossiles" n'a plus varié.

Le prochain satellite Planck, qui prendra la suite de COBE (cf. Cosmic Background Explorer, et Nobel 2006 : John C. Mather & George Smoot) et de W_MAP, donnera la température de ce rayonnement avec une précision de 10^(-6)K, ce qui permettra de voir encore mieux les légères perturbations au moment du "découplage matière-rayonnement" quand les premiers atomes se sont formés. La température actuelle est 2,7283 K environ (cf laboratoire du LERMA, observatoire de Paris).

Loi de Wien

Rappel de l'énoncé de la loi de Wien : le rayonnement émis par le four est nul aux basses fréquences et aux hautes fréquences. Il passe par un maximum pour une fréquence f dite fréquence de Wien variant linéairement avec la température absolue T

L'analyse dimensionnelle donne immédiatement h.f = kT.

Le résultat exact donné par la loi de Planck en fréquence est hf = b. kT ; la valeur numérique b est telle que :b = 3(1-exp(-b)), soit b = 2.822...

Loi exacte du maximum d'émission de Wien

• Si l'on compare avec la courbe de sensibilité des cônes et des bâtonnets de la rétine, on trouve que l'œil humain a subi une "merveilleuse" adaptation à ce créneau du "visible" (pour nous). Les chats ont des habitudes de chasse différentes et donc une autre adaptation. De même, dans l'eau, les animaux rouges se camouflent mieux. L'étude de la vue des rapaces montre aussi une remarquable adaptation.

• Remarque : attention, piège classique : on n'obtient pas la même valeur de b en prenant la loi de Planck en longueur d'onde, comme on pourra aisément le vérifier en regardant l'article corps noir. C'est un piège usuel en théorie des densités de probabilités.

Conclusion

En fait, on a escamoté ici la loi de Planck (cf. corps noir) et tout son historique passionnant. Mais on peut justement par une analyse soigneuse de Dahus montrer comment Planck a réussi à surmonter la contradiction apparente entre la loi de Wien (1896) pour les grandes fréquences et la loi de Jeans-Rayleigh pour les petites : cette subtile analyse est due à Alfred Kastler et mériterait qu'on la publie ici. Superbe aussi est l'analyse de Richard Feynman du <<(n+1)_émis.n(A_excité) pour n_absorbé.n(A_fondamental)>>, qui résume l'essentiel de cette formidable saga scientifique.

L'analyse de la physique en termes simples comme ont su le faire John Archibald Wheeler et Victor Weisskopf et Mr Tompkins (George Gamow), via leurs Dahus, permet ainsi de comprendre beaucoup avec peu de moyens.