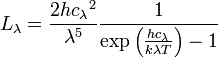Loi de Planck - Définition

Introduction

La loi de Planck définit la distribution de luminance énergétique monochromatique du rayonnement thermique du corps noir en fonction de la température thermodynamique.

La luminance énergétique monochromatique est un flux énergétique par unité de surface, par unité d'angle solide et par unité de longueur d'onde ; elle s'exprime donc en W m^-2.sr^-1m^-1 en unités SI :

c_λ = c / n_λ est la vitesse du rayonnement électromagnétique dans le milieu où se propage le rayonnement, avec :

• n_λ indice de réfraction du milieu pour la longueur d'onde λ
• c = 299 792 458 m/s (vitesse de la lumière dans le vide)
• h = 6,626 17×10^-34 J.s (constante de Planck)
• k = 1,380 66×10^-23 J/K (constante de Boltzmann)
• T est la température de la surface du corps noir en kelvin

Introduction

Un filament d'ampoule à incandescence émet dans le rouge à environ 700 °C, et blanc voire bleu pour des températures supérieures.

La loi de Planck décrit la répartition de l'énergie électromagnétique (ou la répartition de la densité de photons) rayonnée par un corps noir à une température donnée, en fonction de la longueur d'onde . La loi de Planck est présentée sous différentes variantes, qui emploient des grandeurs telle que l'intensité, la densité de flux ou bien la répartition spectrale. Toutes ces formes des différentes grandeurs de rayonnement sont des formes différentes de la loi de Planck.

A la fin du 19è siècle, les physiciens essayaient de comprendre le spectre du rayonnement des corps noirs en se fondant sur la physique classique, la physique statistique et l'électrodynamique classique. Des hypothèses contradictoires (loi de Wien, loi de Rayleigh-Jeans) et une concordance seulement partielle avec les résultats expérimentaux conduisirent à une situation non satisfaisante. C'est Max Planck qui, à la fin du siècle, réussit à trouver une loi de rayonnement complètement en accord avec les mesures expérimentales. Outre l'importance pratique du corps noir, la découverte de la loi de Planck en 1900 signe la naissance de la mécanique quantique : pour expliquer sa loi trouvée de manière empirique, Planck a dû supposer que la lumière (et donc le rayonnement électromagnétique en général) n'était pas absorbée et émise de manière continue, mais uniquement de manière discrète, par l'intermédiaire de quanta (on parle aujourd'hui de photons).

D'après la loi du rayonnement de Kirchhoff, la capacité d'absorption et la capacité d'émission de rayonnement thermique d'un corps sont proportionnels pour toutes les longueurs d'ondes. Un corps noir est un corps hypothétique qui absorbe tout le rayonnement qu'il reçoit, quelle que soit la longueur d'onde. Comme sa capacité d'absorption prend la plus grande valeur possible quelle que soit la longueur d'onde, sa capacité d'émission prend également la plus grande valeur possible. Un corps réel ne peut pas émettre plus de rayonnement thermique qu'un corps noir, car celui-ci représente une source de rayonnement thermique idéale. Comme son spectre ne dépend d'aucun autre paramètre que de la température (en particulier, il ne dépend pas des propriétés du matériau), le corps noir est une source de référence utilisée dans de nombreux cas.

Conséquences

La loi de Planck a unifié et confirmé des lois qui avaient été trouvées précédemment suites à des expériences ou des considérations thermodynamiques :

• la loi de Stefan-Boltzmann, qui donne l'énergie totale rayonnée par un corps noir, proportionnelle à T⁴,
• la loi du rayonnement de Rayleigh-Jeans, qui décrit la distribution spectrale d'énergie pour les grandes longueurs d'ondes,
• la loi du rayonnement de Wien, qui décrit la distribution spectrale d'énergie pour les petites longueurs d'ondes,
• la loi du déplacement, que Wien (1864-1928) formula en 1893, qui établit le rapport entre le maximum d'émission d'un corps noir et sa température.