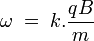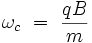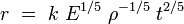Analyse dimensionnelle - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
L'analyse dimensionnelle est un outil théorique servant à interpréter les problèmes à partir des dimensions des grandeurs physiques mises en jeu. Cet outil est utilisé particulièrement en physique, en chimie et en ingénierie. L'analyse dimensionnelle permet notamment de vérifier a priori la viabilité d'une équation ou du résultat d'un calcul. Elle est utile également pour formuler des hypothèses simples sur les grandeurs qui gouvernent l'état d'un système physique avant qu'une théorie plus complète ne vienne valider ces hypothèses.
L'analyse dimensionnelle repose sur le fait que ne peuvent être comparées que des grandeurs ayant la même dimension : il est possible de comparer deux longueurs entre elles, mais pas une longueur et une masse entre elles par exemple. Mathématiquement, cette assertion est fondée sur le théorème de Vaschy-Buckingham.
Étalons, unités et équation aux dimensions
L’équation aux dimensions est la formule qui permet de déterminer la dimension dans laquelle doit être exprimé le résultat d'une formule. C'est une équation de grandeurs, c'est-à-dire dans laquelle on représente les phénomènes mesurés par un symbole ; par exemple, une longueur est représentée par la lettre « L ».
Une grandeur est un paramètre mesurable qui sert à définir un état, un objet. Par exemple, la longueur, la température, l'énergie, la vitesse, la pression, une force (par exemple le poids), l'inertie (masse), la quantité de matière (nombre de moles)… sont des grandeurs.
D'une manière générale il est possible d'exprimer la dimension de toutes les grandeurs physiques en fonction de sept dimensions de bases. Les notations suivantes sont largement répandues :
- longueur L
- masse M
- temps, ou durée T
- intensité électrique I
- température Θ
- énergie rayonnante J
- quantité de matière N
L'on aurait pu choisir sept autres grandeurs de référence, par exemple définir la vitesse comme grandeur de base et définir l'étalon-longueur en fonction de l'étalon-vitesse et de l'étalon-temps (c'est ce qui est d'ailleurs fait implicitement, l'étalon-vitesse étant la vitesse de la lumière dans le vide) ; le choix de ces sept grandeurs est une construction historique, les grandeurs ont été choisies depuis le XVIIIe siècle en fonction des besoins et des étalons que l'on pouvait fabriquer de manière simple et précise. Elles sont a priori les plus basiques et celles que l'on pourra difficilement exprimer en fonction d'autre grandeurs de manière simple.
Ainsi, la dimension d'une grandeur est la manière dont elle se compose à partir des sept dimensions de base. Par exemple, on dit que « la dimension d'une vitesse est une longueur divisée par une durée » (on dit aussi « la vitesse est homogène à une longueur divisée par une durée). On note ceci de manière abrégée par une équation aux dimensions :
La composition peut devenir plus complexe. Ainsi, la force a la dimension d'une masse multipliée par une longueur et divisée par une durée au carré :
-
![\left[ F \right] \; = \; M \cdot \frac{L }{T^2} \; = \; M \cdot L \cdot T^{-2}](https://static.techno-science.net/illustration/Definitions/autres/f/fff8815efc4a7a2e17cd47010f05a705_96bfe4f3a1f0fc520f443e08b61b8b5e.png)
![\left[ F \right] = \frac{M \cdot \left[ V \right]}{T}.](https://static.techno-science.net/illustration/Definitions/autres/6/658dba7130557adfbb76fba62f2b52ef_283be28e9cbebdb36aee1f5165f221b3.png)
Prédictions
L'analyse dimensionnelle permet de trouver la solution de certains problèmes sans avoir à résoudre d'équations grâce au théorème de Buckingham (parfois appelé « théorème Pi »). Deux exemples célèbres sont le calcul de la puissance de la première bombe atomique et le modèle de Kolmogorov de la turbulence homogène isotrope, qui a influencé grandement toute la mécanique des fluides. Ce type de calcul n'est valable que si un petit nombre de paramètres contrôlent la solution d'un problème (2 ou 3).
Illustration de la méthode
Considérons un point matériel de masse m et de charge électrique q soumis à un champ magnétique uniforme
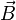

Lorsque
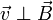
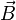
où k, α, β et γ sont des constantes inconnues, et des nombres sans dimension. Les équations aux dimensions permettent de déterminer ces nombres. En effet, on a :
d'où l'équation aux dimensions d'un champ magnétique :
On en déduit l'équation aux dimensions de ω :
Par ailleurs, la vitesse angulaire ω est le rapport d'un angle divisé par un temps T0 (la période de rotation) :
Un angle étant sans dimensions, il vient :
On en déduit que
- γ = 1 ;
-
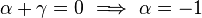
-
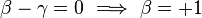
D'où la forme de ω :
On appelle « pulsation cyclotron » la grandeur :
La constante numérique k ne peut pas être déterminée par cette méthode ; il faut faire un calcul explicite complet de ω pour la trouver (ou une mesure expérimentale pour la déterminer). L'expérience montre cependant que, dans un système d'unité adapté au problème étudié, la constante k est toujours de l'ordre de grandeur de 1 (au sens où π ~ e ~ 1), d'où la pertinence de l'analyse dimensionnelle pour prévoir la forme du résultat d'un calcul, ainsi que son ordre de grandeur.
« Principe zéro » de la physique théorique
La puissance du pouvoir prédictif de l'analyse dimensionnelle en regard de sa simplicité a conduit Wheeler à proposer le principe général suivant :
- « Ne jamais faire de calculs avant d'en connaître le résultat. »
Cet énoncé, qui peut sembler a priori paradoxal, signifie concrètement : ne pas se lancer dans un calcul compliqué sans avoir trouvé au préalable la forme qualitative du résultat avec l'analyse dimensionnelle.
Exemple : un calcul de G.Taylor
La légende voudrait que l'analyse dimensionnelle ait permis à Geoffrey Ingram Taylor d'estimer en 1950 l'énergie dégagée par l'explosion d'une bombe atomique, alors que cette information était classée top secret. Il lui a suffi pour cela d'observer sur un film d'explosion, imprudemment rendu public par les militaires américains, que la dilatation du champignon atomique suivait la loi expérimentale de proportionnalité.
note 1 : en réalité, la solution qui suit a été trouvée indépendamment par Geoffrey Ingram Taylor et John von Neumann durant la seconde guerre mondiale . Après la guerre, cette solution a été publiée par trois autres auteurs — L. I. Sedov, R. Latter, et J. Lockwood-Taylor. En 1949, suite à la déclassification des images d'une explosion nucléaire au Nouveau Mexique, Taylor analyse les photographies à la lumière de ses travaux passés et en déduit la puissance de la bombe.
La légende est la suivante : Le physicien Taylor suppose a priori que le processus d'expansion de la sphère de gaz dépend au minimum des paramètres suivants :
- le temps t ;
- l'énergie E dégagée par l'explosion ;
- la masse volumique de l'air ρ.
L'analyse dimensionnelle le conduit alors pour le rayon de la sphère de gaz à l'instant t à :
où k est une constante sans dimensions. Taylor retrouve donc bien la loi expérimentale de dilatation du champignon
-
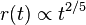
ce qui semble valider son choix de paramètres. Il détermine alors r et t à partir du film, et, k étant supposée de l'ordre de l'unité et ρ étant connue, il obtient finalement :
note 2 : En réalité, G. I. Taylor n'a pas utilisé ce raisonnement simpliste. Dans sa première publication, longue de 15 pages, G. I. Taylor utilise l'analyse dimensionnelle pour simplifier les équations différentielles qui décrivent l'écoulement. Après de long et difficiles calculs, il obtient finalement la formule très simple suivante :
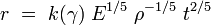
note 3 : l'expression de l'énergie dans l'exemple ci-dessus (bombe nucléaire) peut être obtenue de manière plus générale sans faire référence à l'expansion d'une sphère de gaz.Puisqu'il s'agit de retrouver rapidement le monôme qui intervient dans la relation
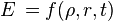
![E=mc^2 \Rightarrow [E]= M.L^2.T^{-2}](https://static.techno-science.net/illustration/Definitions/autres/5/5a6387a722cc27d2a40c29d9429f0479_c06de3d79ffde98f2a9c98c392b9f9f7.png)
![\rho= \frac{m}{V} \Rightarrow [\rho]= M.L^{-3}](https://static.techno-science.net/illustration/Definitions/autres/0/0472eace69ddcb8af6177f7708bbe3c2_cb1be35be22ce4537a3a065ac600faf5.png)
![\frac {[E]}{[\rho]} = L^5.T^{-2}](https://static.techno-science.net/illustration/Definitions/autres/a/acac67ab2a3e5b602c095fdc57ce53cc_6e92ee5e28507ed0960534d60307e989.png)
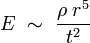
![\left[ V \right] \; = \; \frac{L}{T}.](https://static.techno-science.net/illustration/Definitions/autres/a/acd2cda36f209ea0b451ae471b0d75e3_048c67b9475070cb1aa4ab09288470c0.png)
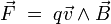
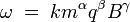
![\left[ F \right] \; = \; M.L.T^{-2} \; = \; \left[ q.v.B \right] \; = \; Q.L.T^{-1} \; \left[ B \right]](https://static.techno-science.net/illustration/Definitions/autres/9/93b95313c4812ec2fdd9602970c7aeec_088b69732244e02de1da4fe661fe2d06.png)
![\left[ B \right] \; = \; M.T^{-1}.Q^{-1}](https://static.techno-science.net/illustration/Definitions/autres/d/df33a0a3caaafa8d70354392fbd5b0d1_d404fe155fdf1ff01d87da515645b1a2.png)
![\left[ \ \omega \ \right] \ = \ \left[ \ k \; m^{\alpha} \; q^{\beta} \;B^{\gamma} \ \right] \ = \ M^{\alpha} \; Q^{\beta} \; \left[ \ B\ \right]^{\gamma} \ = \ M^{\alpha+ \gamma} \; Q^{\beta - \gamma} \; T^{-\gamma}](https://static.techno-science.net/illustration/Definitions/autres/4/4c64f24b3d0cb0c109061f820b732060_8be09fc90a8b6d0916c0f49930573d57.png)
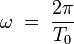
![\left[ \omega \right] \; = \; T^{-1} \; = \; M^{\alpha+ \gamma}.Q^{\beta - \gamma}.T^{-\gamma}](https://static.techno-science.net/illustration/Definitions/autres/7/7559c27f0d6ab9a721136a7e702ef027_5a92cdc24127ecdb7d70d1c9e2460f53.png)