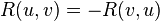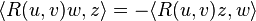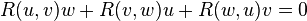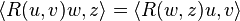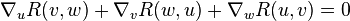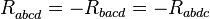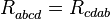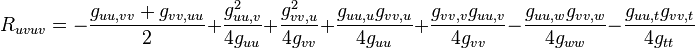Tenseur de Riemann - Définition

Symétries et identités

Le tenseur de courbure de Riemann a les symétries suivantes :

La dernière identité a été découverte par Ricci, mais est souvent nommé première identité de Bianchi ou identité algébrique de Bianchi.

Ces trois identités forment une liste complète des symétries de tenseur de courbure, c'est-à-dire qu'étant donné un tenseur respectant les identités ci-dessus, on peut trouver une variété de Riemann disposant d'un tel tenseur de courbure en un point. De simples calculs mathématiques montrent qu'un tel tenseur a n²(n² − 1) / 12 composants indépendants.

Il est possible de déduire une autre identité utile à partir de ces trois équations :

L'identité de Bianchi (souvent appelée seconde identité de Bianchi ou identité différentielle de Bianchi) implique les dérivées covariantes :

Étant donné un référentiel donné en un point d'une variété, les identités précédentes peuvent être écrites en termes des composants du tenseur de Riemann comme :

(première identité de Bianchi)

(seconde identité de Bianchi)

où les crochets correspondent au crochet de Lie, qualifiant les symétrisations selon les indices, et le point-virgule représente la dérivée covariante.

Tenseur de Riemann d'un espace à quatre dimensions

Une surface est plongée dans notre espace à trois dimensions. Lorsqu'on ajoute deux dimensions, on obtient une hypersurface à quatre dimensions (u,v,w,t) plongée dans un espace à cinq dimensions. Pour obtenir le tenseur de Riemann de cet espace, on rajoute deux termes supplémentaires dans l'expression du tenseur de Riemann d'une surface qui devient

Le tenseur de Riemann d'une métrique diagonale a six composantes non nulles R_uvuv, R_uwuw, R_vwvw,pour l'espace à trois dimensions plus R_utut, R_vtvt, R_wtwt, pour l'extension à quatre dimensions.