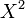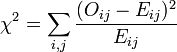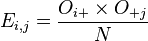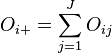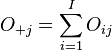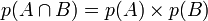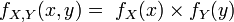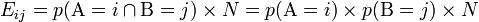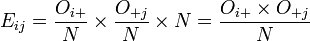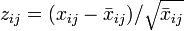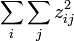Test du ?² - Définition
La liste des auteurs de cet article est disponible ici.
Utilisations possibles
Test du χ² d'adéquation
Généralités
Il s'agit de juger de l'adéquation entre une série de données statistiques et une loi de probabilité définie a priori (comme une loi uniforme ou une loi de Poisson par exemple).
Exemple concret : Soit un nombre donné de cultures cellulaires rigoureusement identiques. Chacune comporte un certain nombre de colonies. Toutes les cultures sont en fait des cultures de cellules cancéreuses et on cherche à déterminer dans quelle mesure l'action d'un produit empêche leur division. Précisément on veut savoir si le nombre de colonies dont la croissance sera interrompue par le produit suit une loi de Poisson de paramètre λ.
Après avoir exposé les cellules au produit, on obtient des résultats précis: X colonies de la première culture ont subi l'influence du produit, X pour la deuxième culture... X pour la n-ième culture. On effectuera un test du χ² sur ces valeurs pour juger l'hypothèse selon laquelle leur distribution suit une loi de Poisson.
Description
La statistique mathématique a pour but la description d'une population dont on ne connaît qu'un nombre relativement petit d'individus. Pour cela on associe une loi de probabilité à cette population. Mis à part certains problèmes de physique fondamentale et, à l'opposé, certains problèmes élémentaires (jeux de hasard équitables, par exemple), cette loi de probabilité est en toute rigueur inconnue. L'hypothèse selon laquelle la population suit une loi de probabilité donnée a priori peut être testée par la méthode décrite ci-après.
Lorsqu'on découvre un élément de la population, celui-ci est considéré comme une réalisation d'une variable aléatoire correspondant à la loi de probabilité choisie. Plus généralement, un ensemble d'éléments est une réalisation de ce qu'on appelle un échantillon aléatoire.
Les valeurs connues doivent être réparties entre diverses classes. En supposant l'indépendance des
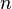
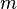
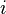
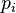
Les effectifs mesurés étant
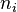
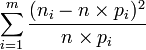
Il est peu vraisemblable que les paramètres qui caractérisent la loi de probabilité (moyenne, variance, ...) soient connus au moment du test. Les données sont donc utilisées pour estimer ceux-ci, ce qui facilite l'adéquation. Il faut alors diminuer le nombre de degrés de liberté du nombre de paramètres estimé.
Choix des classes
Celles-ci doivent être assez nombreuses pour ne pas perdre trop d'information mais, à l'inverse, pour satisfaire les conditions requises par la méthode, elles ne doivent pas être trop petites. En théorie, il faudrait que les effectifs soient infinis pour que la loi normale s'applique mais il est généralement admis qu'il faut 5 éléments dans chaque classe. Cette règle a été très discutée et celle qui semble recueillir le plus de suffrages est due à Cochran : 80 % des classes doivent satisfaire la règle des cinq éléments tandis que les autres doivent être non vides.
Le critère porte sur les
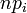
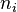
Test du χ² d'homogénéité
Il s'agit alors de se demander si deux listes de nombres de même effectif peuvent dériver de la même loi de probabilité. La méthode précédente s'applique en remplaçant le terme
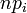
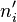
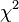
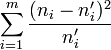
Cette notation s'inspire de celle utilisée pour le test d'adéquation, elle-même déduite de la notation classique de la loi multinomiale. Ici, comme dans le test d'indépendance, la notion de probabilité n'apparaît plus de manière explicite. De nombreux utilisateurs préfèrent donc adopter la notation qui utilise les symboles
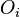
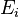
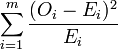
Test du χ² d'indépendance
Exemple
Problème
Lorsqu'on considère plusieurs populations auxquelles on associe le même ensemble de critères qualitatifs, l'hypothèse à tester est l'indépendance de ces populations.
Pour ce problème, il est commode de partir d'un exemple concret, comme la relation entre le revenu et le sexe d'un individu. La distribution du revenu des hommes est-elle différente de celui des femmes ? Une représentation sur une table de contingence des occurrences des variables permet d'illustrer la question.
| Salaire | 1000-2000 | 2000-3000 | 3000-4000 | 4000-5000 | Total |
|---|---|---|---|---|---|
| Hommes | 50 | 70 | 110 | 60 | 290 |
| Femmes | 60 | 75 | 100 | 50 | 285 |
| Total | 110 | 145 | 210 | 110 | 575 |
Dans cet exemple fictif on remarque que les femmes sont plus nombreuses dans les classes à bas salaires et moins nombreuses dans celles à haut salaire que les hommes. Cette différence (c’est-à-dire cette dépendance entre les variables) est-elle statistiquement significative ? Le test du χ² aide à répondre à cette question.
Préparation
On peut constater que l'effectif total de chaque colonne correspond à 4-1 = 3 variables indépendantes tandis que celui de chaque ligne correspond à 2-1 = 1 variables indépendantes, ce qui conduit à 3 x 1 = 3 degrés de liberté.
Si on se donne un risque de se tromper égal à 5 %, la valeur critique trouvée dans les tables est 7,81.
Hypothèse
Il faut bâtir l'hypothèse nulle qui, dans ce cas, ne dépend ni d'une loi de probabilité, ni d'une distribution de référence. On suppose qu'il n'y a pas de différence entre les salaires des hommes et ceux des femmes, les proportions des différentes catégories de salaires étant donc conservées d'une ligne à l'autre.
Les données correspondantes sont obtenues en remplaçant la valeur de chaque cellule par le produit du total de sa ligne par le total de sa colonne divisé par le total général. On vérifie que les totaux sont inchangés.
| Hypothèse | 1000-2000 | 2000-3000 | 3000-4000 | 4000-5000 | Total |
|---|---|---|---|---|---|
| Hommes | 55,5 | 73,1 | 105,9 | 55,5 | 290,0 |
| Femmes | 54,5 | 71,9 | 104,1 | 54,5 | 285,0 |
| Total | 110,0 | 145,0 | 210,0 | 110,0 | 575,0 |
Calcul
Le calcul du χ² des données s'effectue en remplaçant le terme relatif à chaque cellule par la quantité
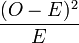
|
| 1000-2000 | 2000-3000 | 3000-4000 | 4000-5000 | Total |
|---|---|---|---|---|---|
| Hommes | 0,54 | 0,13 | 0,16 | 0,37 | 1,20 |
| Femmes | 0,55 | 0,14 | 0,16 | 0,38 | 1,23 |
| Total | 1,09 | 0,27 | 0,32 | 0,75 | 2,43 |
Conclusion
La distance calculée (2,43) étant inférieure à la distance critique (7,81), il n'y a pas lieu de mettre en cause l'égalité des salaires, avec un risque de se tromper égal à 5%.
Il convient de rappeler que ce résultat repose sur des données choisies arbitrairement qui ont... peu de chance de représenter une réalité quelconque. D'autre part, si on disposait d'un échantillon 10 fois plus grand sans modification de la répartition de population, le χ² serait multiplié par 10, soit (24,3) et on pourrait rejeter l'hypothèse d'égalité avec moins de 5% de risque de se tromper.
De manière plus profonde, les classes choisies, à la différence de ce qui se passait dans les tests d'adéquation et d'homogénéité, bien que présentant ici un aspect numérique, pourraient fort bien être associées à des notions qualitatives sans que le raisonnement soit modifié.
Test utilisé
Le test utilisé, le Chi-carré de Pearson, s'intéresse à la différence entre la valeur observée O (ou valeur empirique) et la valeur attendue s'il y avait indépendance E (ou valeur théorique).
avec
- O la valeur observée
- E la valeur attendue sous l'hypothèse d'indépendance.
On a :
où
et
Formulation du test
H :
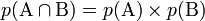
H :
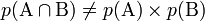
Distribution du test
Cette statistique suit asymptotiquement une Loi du χ² à (I-1)(J-1) degrés de liberté, avec I le nombre de modalités de la première variable et J les nombre de modalités de la seconde variable.
Conditions du test
Plusieurs auteurs proposent des critères pour savoir si un test est valide, voir par exemple [pdf] The Power of Categorical Goodness-Of-Fit Test Statistics p. 19 (p. 11 du ch. 2), Michael C. Steele. On utilise en général le critère de Cochran de 1954 selon lequel toutes les classes i, j doivent avoir une valeur théorique non nulle (E ≥ 1), et que 80 % des classes doivent avoir une valeur théorique supérieure ou égal à 5 :
- E ≥ 5
Lorsque le nombre de classes est petit, cela revient à dire que toutes les classes doivent contenir un effectif théorique supérieur ou égal à 5.
D'autres valeurs ont été proposées pour l'effectif théorique minimal : 5 ou 10 pour tous (Cochran, 1952), 10 (Cramér, 1946) ou 20 (Kendall, 1952). Dans tous les cas, ces valeurs sont arbitraires.
Certains auteurs ont proposé des critères basés sur des simulations, par exemple :
- effectif théorique supérieur à 5r/k pour chaque classe, où r est le nombre de classes ayant un effectif supérieur ou égal à 5 et k est le nombre de catégories (Yarnold, 1970) ;
- N²/k ≥ 10, où N est l'effectif total et k est toujours le nombre de catégories (Koehler et Larntz, 1980). Pour voir recommedations plus récentes on peut regarder, par exemple, P. Greenwood and M. Nikulin "A Guide to Chi-Squared Testing", (1996), John Wiley and Sons.
Tests apparentés
Il existe un test asymptotique très semblable, le test du rapport de vraisemblance (likelihood ratio test), ainsi qu'un test exact, le test de Fisher.
Justification
Le développement des méthodes bayésiennes - seules utilisables lorsqu'on n'a que peu de données sous la main - a dégagé un test de vraisemblance nommé le psi-test, dont Myron Tribus fait remarquer qu'il devient asymptotiquement identique au χ² à mesure que le nombre de données augmente.
Indépendance
Soient A et B les deux variables dont on souhaite tester l'indépendance.
Pour rappel, si A et B sont indépendantes on a la relation suivante :
ou pour la fonction de densité conjointe :
Soit ici
Estimation des valeurs attendues (théoriques)
Que vaut p(A=i ) ?
À partir de la table de contingence, on prendra simplement la somme de toutes les valeurs où A = 1, soit, dans notre notation
- O
Ainsi
Distribution du test
Pour la preuve que le test suit une loi Chi-carré, on en donnera ici que quelques « pistes ».
Si on suppose que chaque x suit une loi de Poisson, on peut montrer que les valeurs standardisées
suivent asymptotiquement une loi normale. Alors
suit asymptotiquement une loi Chi-carré à IJ-1 degrés de liberté
Quant aux degrés de libertés, comme on doit estimer les
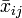
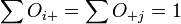
- IJ-1-(I-1)-(J-1) = I(J-1)-(J-1) = (I-1)×(J-1)