Statistique mathématique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Les statistiques, dans le sens populaire du terme, traitent des populations. En statistique descriptive, on se contente de décrire un échantillon à partir de grandeurs comme la moyenne, la médiane, l'écart type, la proportion, la corrélation, etc. C'est souvent la technique qui est utilisée dans les recensements.
Dans un sens plus large, la théorie statistique est utilisée en recherche dans un but inférentiel. Le but de l'inférence statistique est de dégager le portrait d'une population donnée, à partir de l'image plus ou moins floue constituée à l'aide d'un échantillon issu de cette population.
Dans un autre ordre d'idées, il existe aussi la statistique « mathématique » où le défi est de trouver des estimateurs judicieux (non biaisées et efficients). L'analyse des propriétés mathématiques de ces estimateurs sont au cœur du travail du mathématicien spécialiste de la statistique.
Statistique
La statistique mathématique repose sur la théorie des probabilités. Des notions comme la mesurabilité ou la convergence en loi y sont souvent utilisées. Mais il faut distinguer la statistique en tant que discipline et la statistique en tant que fonction des données.
Une fois les bases de la théorie des probabilités acquises, il est possible de définir une statistique à partir d'une fonction S mesurable à n arguments. Lorsque les valeurs
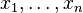
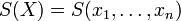
La loi de S(X) dépend uniquement de la loi de X et de la forme de S.
Fonctions de répartition
La fonction de répartition d'une variable aléatoire réelle X (cette définition s'étend naturellement aux variables aléatoires à valeurs dans des espaces de dimension quelconque) associe à une valeur x la probabilité qu'une réalisation de X soit plus petite de x :
F(x) = Prob(X < x)
Lorsqu'on dispose de n réalisations de X, on peut construire la fonction de répartition empirique de X ainsi (on note x(k) la kème valeur ordonnées des
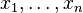
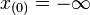
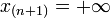
![F^*_n(x) = {k\over n},\, \forall x\in ]x_{(k)},x_{(k+1)}]](https://static.techno-science.net/illustration/Definitions/autres/b/be897bb86ca1ce37f497a43c6ecdc5da_d175574932961338e1d71a9e14d8b271.png)
de même, la distribution empirique peut se définir (pour tout borélien B) comme :
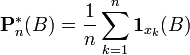
Le Théorème de Glivenko-Cantelli assure la convergence de la fonction de distribution empirique vers la fonction de distribution original lorsque la taille n de l'échantillon augmente vers l'infini.
Ces deux fonctions empirique n'étant pas continues, on leur préfère souvent des estimateurs par noyau, qui ont les mêmes propriétés de convergence.
Types de statistiques
On définit usuellement plusieurs types de statistiques suivant la forme de S :
- les L-statistiques qui sont des combinaisons de statistiques d'ordres,
- les M-statistiques qui s'expriment comme le maximum d'une fonction des réalisations d'une variable aléatoire,
- les U-statistiques qui s'expriment sous la forme d'intégrales.
L'intérêt de cette différenciation est que chaque catégorie de statistique va avoir des caractéristiques propres.
Les estimateurs par noyau, et les moments empiriques d'une loi sont les M-statistiques.
Le moment empirique d'ordre k d'une loi calculé à partir d'un échantillon
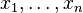
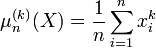
Il s'agit d'un estimateur de E(Xk). Le moment centré d'ordre k est E((X − E(X))k). La variance est le moment centré d'ordre 2.
Estimation
Ces résultats s’interprètent directement en termes d’estimation.
- La moyenne empirique et la variance empirique fournissent des estimations de la moyenne et de la variance de la population.
- Ces estimations sont convergentes car leurs variances tendent vers zéro lorsque la taille de l’échantillon s’accroît indéfiniment.
- Elles sont non biaisées car leur limite est égale à la valeur à estimer.
Le problème d’estimation est relié aux intervalles de confiance. L’idée est de fournir une estimation d’un paramètre accompagnée d’une idée de sa précision liée aux fluctuations échantillonnales.
Voici un exemple bien spécifique d’intervalle de confiance pour la moyenne.
Pour décrire le principe, considérons un exemple assez artificiel qui présente l’avantage de la simplicité : l’estimation de la moyenne (m) d’une population supposée normale dont nous connaîtrions l’écart-type (σ). D’après le paragraphe précédent, la moyenne empirique suit également une loi normale dont l’écart-type est divisé par le facteur
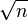
Puisque les tables de probabilités de la loi normale sont connues, nous pouvons déterminer qu’un intervalle centré autour de la moyenne empirique aura x % de chance de contenir la vraie moyenne. En pratique, x est souvent fixé à 95. Lorsqu’on fixe x (à 95 par exemple), on détermine la longueur de l’intervalle de confiance simplement par connaissance de la loi normale. Voici l’intervalle de confiance à 95 % pour ce cas très précis.
![[m - {{1.96 \sigma}\over \sqrt n}\ ; m + {{1.96 \sigma}\over \sqrt n}]](https://static.techno-science.net/illustration/Definitions/autres/7/7e5cfae70b4f1ddbbd8036eb1907b0e6_137a914c9ca9ddeefe65a4aec14c734a.png)
voir aussi loi de Student.

















































