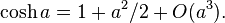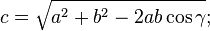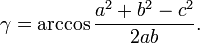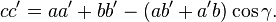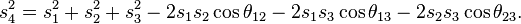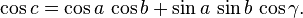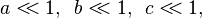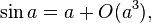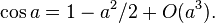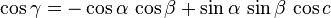Théorème d'Al-Kashi - Définition

Le théorème et ses applications

Le théorème d'Al-Kashi est également connu sous le nom de théorème de Pythagore généralisé, car le théorème de Pythagore en est un cas particulier :

L'angle γ est droit (autrement dit lorsque cos γ = 0) si et seulement si d'après le théorème d'Al-Kashi.

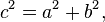
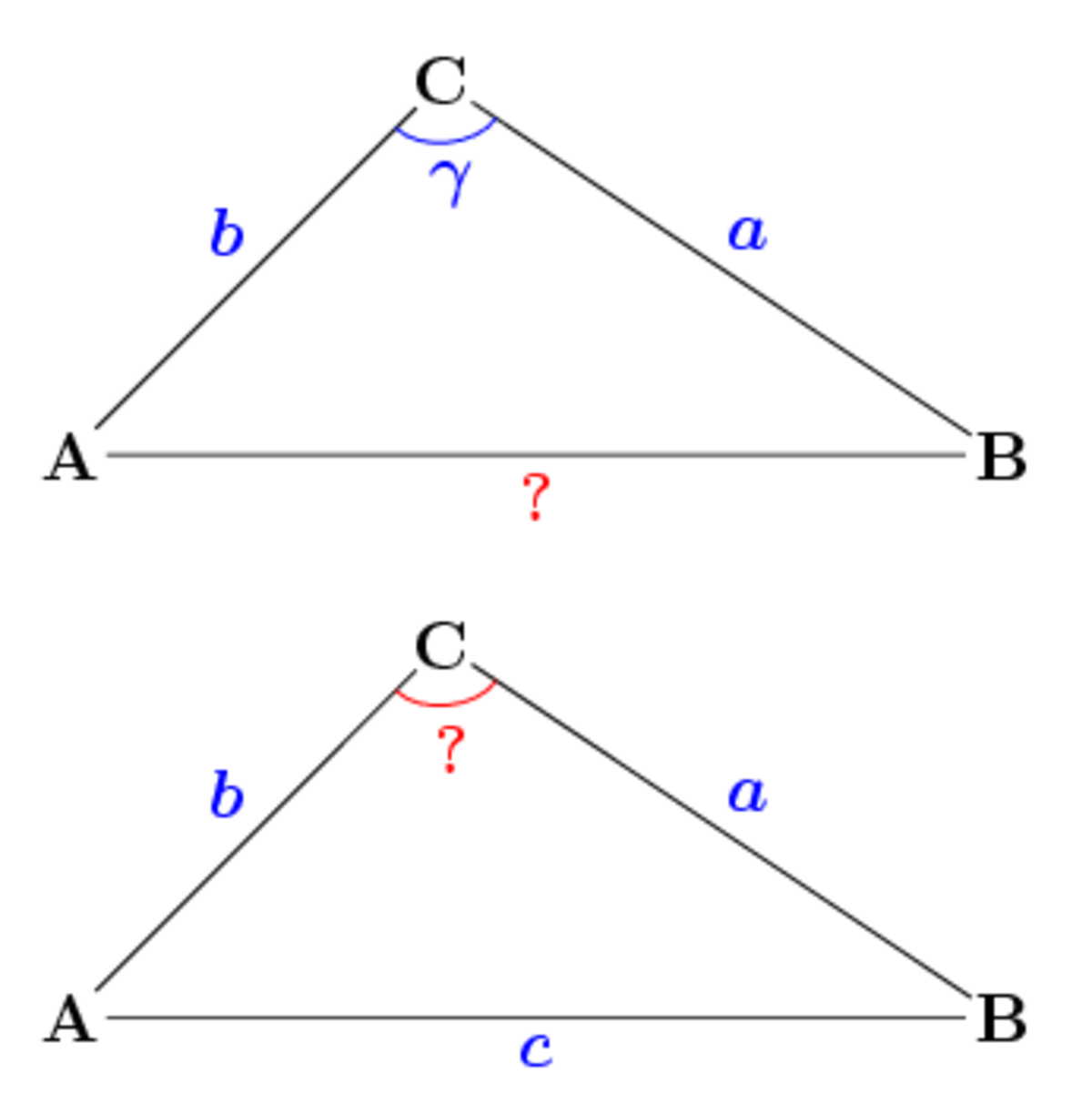
Le théorème s'utilise en triangulation (voir Fig. 3) pour résoudre un triangle, à savoir déterminer

• le troisième côté d'un triangle dont on connaît un angle et les côtés adjacents :

• les angles d'un triangle dont on connaît les trois côtés :

Ces formules sont instables numériquement dans le cas de triangles en épingle, c'est-à-dire lorsque c est petit devant a et b — ou, de façon équivalente, lorsque γ est petit devant 1.

Il existe un corollaire du théorème d'al-Kashi : pour deux triangles directement semblables ABC et A'B'C'

Généralisation à l'espace euclidien

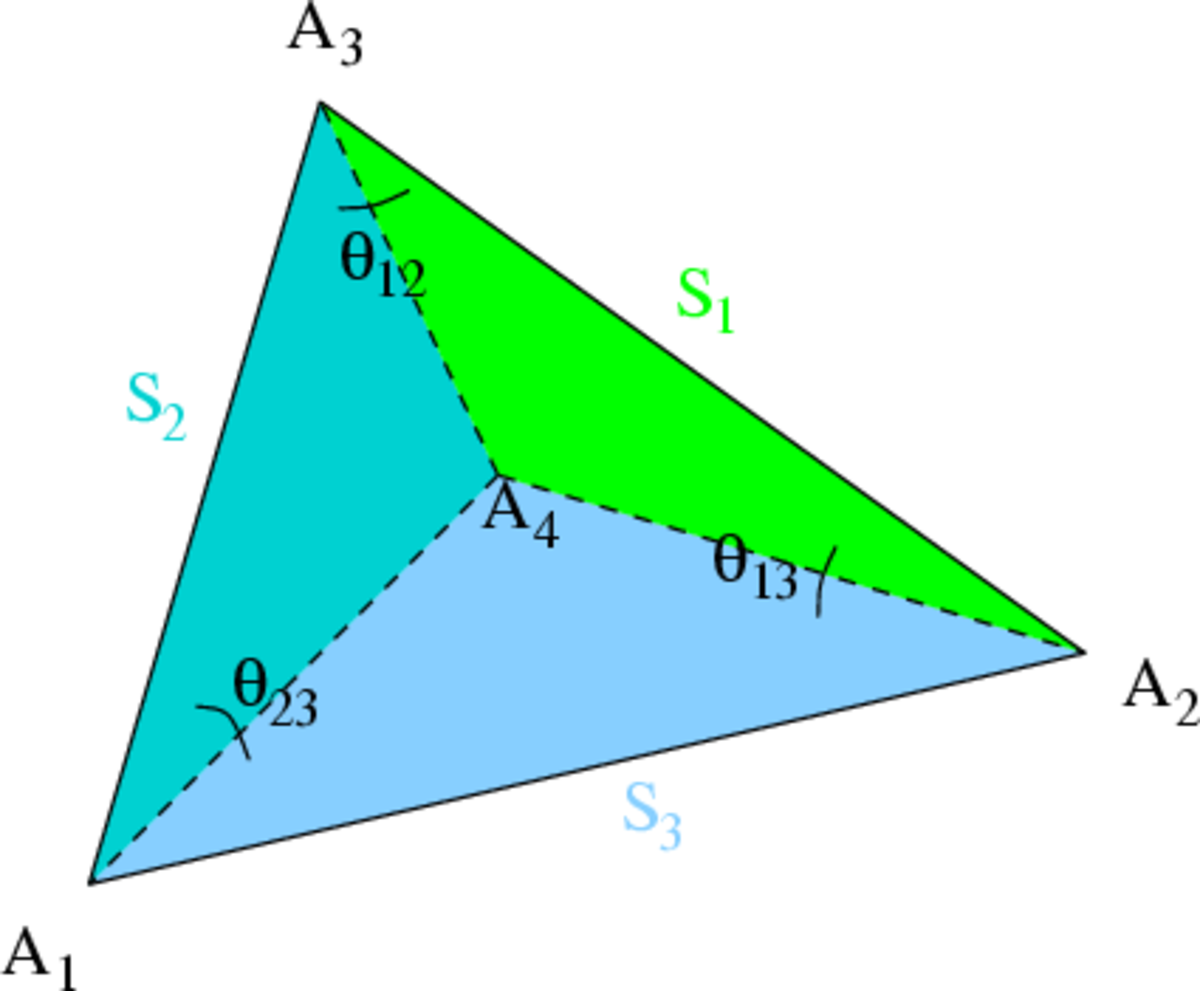
On considère un tétraèdre A₁A₂A₃A₄ de l'espace euclidien. La figure 10 ci-contre présente les notations concernant les sommets, faces et angles dans le tétraèdre :

• S_k la face opposée au sommet ;
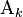
• s_k la surface de ;
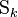
• Δ_k le plan dans lequel est plongée ;
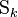
• θ_ij l'angle diédral (Δ_i,Δ_j).

Alors, surfaces et angles vérifient  :

Généralisation aux géométries non euclidiennes

Pour une surface non euclidienne de courbure K, on note R le rayon de courbure. Il vérifie

.

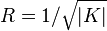
On définit alors les dimensions réduites du triangle :

,

,

.

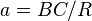
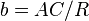
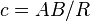
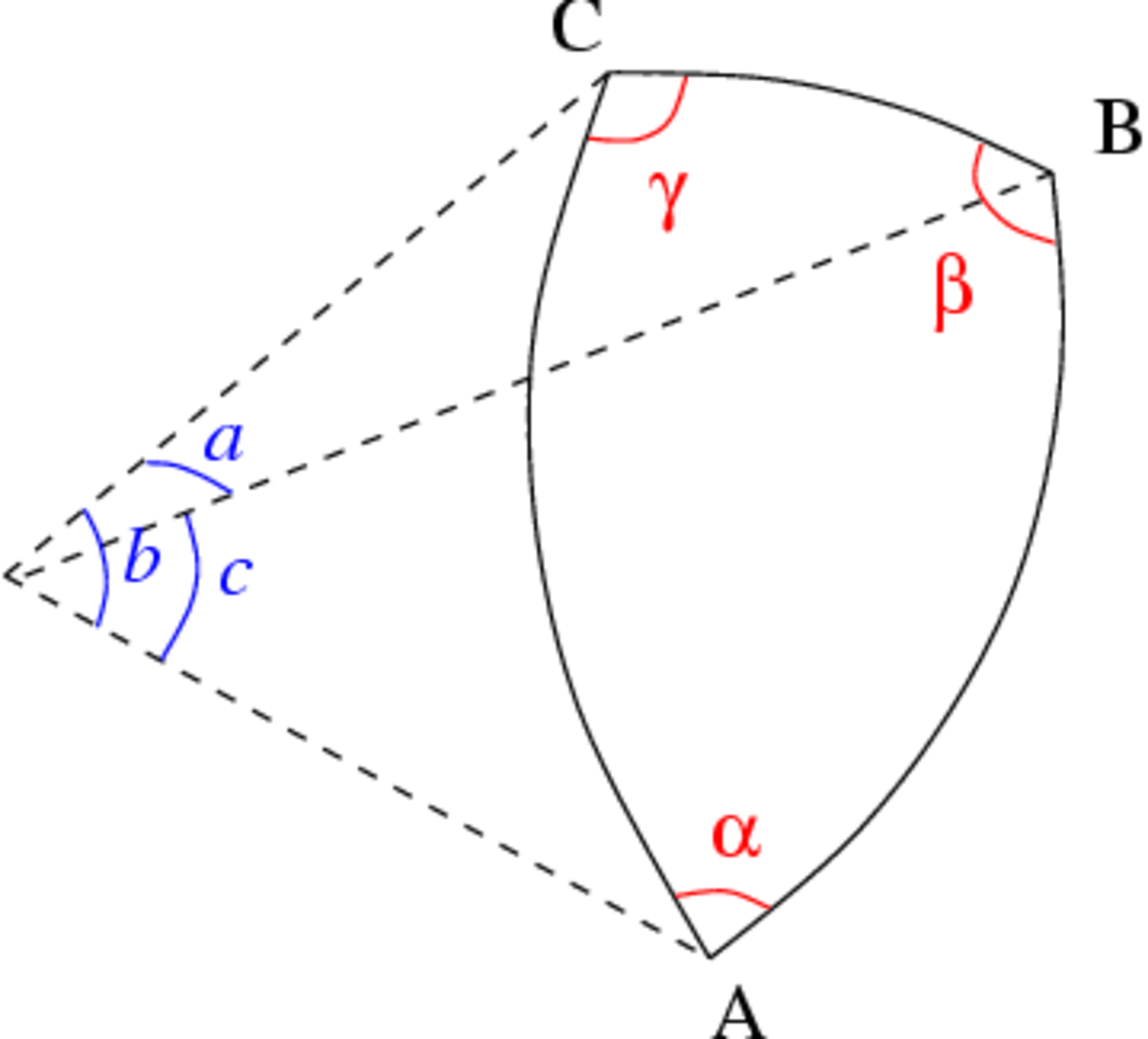
Dans le cas d'un triangle sphérique, a, b et c correspondent à la mesure angulaire des segments de grand arc [BC], [AC] et [AB] (voir Fig. 7).

Géométrie sphérique

Dans un triangle sphérique ABC (Fig. 9), le théorème d'Al-Kashi s'écrit

Lorsque le rayon de courbure est très grand devant les dimensions du triangle, c’est-à-dire lorsque

cette expression se simplifie pour donner la version euclidienne du théorème d'Al-Kashi. Pour le montrer, on utilise les développements limités suivants :

Il existe une identité similaire qui relie les trois angles :

Géométrie hyperbolique

Dans un triangle hyperbolique ABC, le théorème d'Al-Kashi s'écrit

.

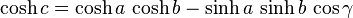
Lorsque le rayon de courbure devient très grand devant les dimensions du triangle, on retrouve le théorème d'Al-Kashi euclidien à partir des développements limités

,
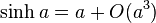