Théorème de Maschke - Définition

Applications

• Ce théorème simplifie la théorie des représentations d'un groupe fini ou des K-algèbre d'un groupe fini. En effet, il suffit de se limiter aux représentations irréductibles. Les autres se déduisent directement par somme directe.

• Il démontre qu'une représentation correspond à une structure d'algèbre semi-simple. Cette remarque permet d'étudier une représentation sous un autre angle, celui des algèbres de groupe.

• Ce théorème permet de démontrer simplement que tout groupe abélien d'ordre fini est un produit de cycles. Le Lemme de Schur prouve que les seules représentations irréductibles sont de degré un. Il suffit alors de considérer la représentation régulière qui possède pour base le groupe lui-même sur le corps des complexes et d'appliquer le théorème de Maschke pour conclure. Une démonstration complète est donnée dans l'article Diagonalisation.

Histoire

Le théorème voit le jour dans le contexte du développement de la théorie des représentations d'un groupe fini. Le mois d'avril 1896 voit dans trois réponses épistolaires de Frobenius à Richard Dedekind la naissance de cette théorie. L'auteur comprend immédiatement qu'il est à l'origine d'une vaste théorie. Le 16 juillet, il publie un premier article. On peut y lire je développerais ici le concept (de caractère pour un groupe fini quelconque) avec la croyance que, à travers cette introduction, la théorie des groupes sera substantiellement enrichie.

L'école de mathématiques de l'Université de Chicago étudie aussi ce sujet, avec un accent particulier sur les corps finis, un de ses membres, Heinrich Maschke , élève de Felix Klein travaille sur le cas des caractères du groupe symétrique. En 1898, il démontre un cas particulier de ce qui deviendra son théorème. Il trouve la preuve générale l'année suivante et elle est publiée dans les Annales mathématiques que dirige Klein. Un mathématicien allemand Alfred Loewy énonce, sans preuve, un résultat analogue au théorème en 1896.

En 1907 à Édimbourg Joseph Wedderburn publie son article peut-être le plus célèbre, classifiant toutes les algèbres semi-simples, la formulation du théorème s'en trouve modifiée.

Exemple le groupe symétrique d'indice trois

Soit (V, ρ) la représentation régulière du groupe S₃ du groupe symétrique d'un ensemble de trois éléments. Le groupe S₃ contient six éléments et trois classes de conjugaison, la première ne contient que l'identité noté 1, la deuxième les transpositions t₁ = (23), t₂ = (13) et t₃ = (12) et la troisième les deux cycles d'ordre trois c₁ = (123) et c₂ = (132). Si V est l'espace vectoriel de la représentation régulière, alors (1, c₁, c₂, t₁, t₂, t₃) est la base canonique de la représentation, à l'ordre près.

On remarque l'existence de deux vecteurs propres pour toutes les images de ρ :

Toute permutation laisse f₁ invariant, toute permutation paire laisse f₂ invariant et toute permutation impaire transforme f₂ en -f₂.

Tout sous-espace vectoriel stable possède un supplémentaire stable, le théorème de Maschke indique une méthode pour le trouver. Soit F l'espace vectoriel engendré par f₁ et f₂ et p le projecteur sur F parallèlement à l'espace engendré par c₁, c₂, t₁, t₂, alors le projecteur p₀ défini par l'égalité suivante possède un noyau stable par toutes les images de ρ.

Dans la base canonique, on obtient les matrices P et P_s des deux projecteurs :

Notons G le noyau de p₀ si j désigne la racine cubique de l'unité, alors on obtient la base suivante de G

Considérons alors la représentation (G, φ) où φ est la restriction de ρ à G. Si G_x est la matrice de φ_x dans la base (g_i) pour x élément de S₃, on obtient :

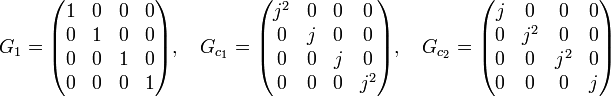
On peut vérifier ensuite que les sous-espaces H₁=1+g₄,g₂+g₃> et H₂=1-g₄,g₂-g₃> sont des sous-espaces stables, supplémentaires dans G. La décomposition en sous-espaces irréductibles prédite par le théorème de Maschke est alors :