Théorème de l'application conforme - Définition

Énoncé du théorème

Plusieurs formulations équivalentes du théorème sont possibles ; on l'énonce généralement ainsi :

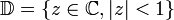
Utilisant les propriétés caractéristiques des fonctions holomorphes (en particulier le fait que, dans C, f dérivable implique f analytique), on peut encore reformuler le théorème en disant qu'il existe une bijection dérivable (dans C) de U vers  ; comme la dérivée d'une bijection holomorphe n'est jamais nulle, on en déduit que la bijection réciproque f ^{− 1} est également holomorphe.

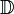
Comme les fonctions holomorphes "conservent les angles", cela revient à dire, d'un point de vue géométrique, qu'il existe une bijection conforme entre U et . Le composé de deux fonctions holomorphes étant holomorphe, on voit qu'en fait, plus généralement, il existe une bijection conforme entre deux ouverts quelconques U et V satisfaisant les hypothèses précédentes.

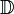
Henri Poincaré a montré que l'application f (entre U et ) est essentiellement unique : si z₀ appartient à U et si φ est un angle arbitraire, il existe exactement une bijection holomorphe f telle que f(z₀) = 0 et que l'argument de la dérivée f'(z₀) soit φ. Ce résultat découle facilement du lemme de Schwarz.

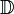
Détermination explicite de bijections conformes

Dans certains cas, il est possible d'obtenir explicitement les bijections dont l'existence est affirmée par le théorème, soit sous forme de transformations géométriques (ainsi, la projection stéréographique est conforme ; la composition de telles projections est une transformation de Möbius), soit par des méthodes relevant de la théorie du potentiel. Voici une liste des cas que l'on sait traiter :

Esquisses de démonstrations

L'historique aura montré qu'il est difficile de donner des démonstrations rigoureuses ; dans le cas où la frontière de l'ouvert est suffisamment régulière, il est relativement aisé d'en donner une démonstration complète ; mais, comme pour le théorème de Jordan, ce cas est nettement plus facile à traiter que le cas général. Une démonstration générale peut cependant être esquissée grâce aux familles normales (dues à Paul Montel) ; suivant Walter Rudin, on commence par

Conséquences et généralisations

On a déjà signalé qu'en fait, le théorème implique que deux ouverts du plan, simplement connexes, non vides et distincts du plan entier, peuvent être mis en en bijection conforme ; la projection stéréographique étant une application conforme, il en est de même des ouverts simplements connexes de la sphère ne contenant pas au moins deux points de celle-ci. Plus généralement encore, on en déduit le théorème d'uniformisation de Riemann : toute surface de Riemann simplement connexe est conforme à l'une des trois surfaces de référence que sont le disque unité, le plan complexe, et la sphère de Riemann. En particulier, toute surface de Riemann simplement connexe compacte est conforme à la sphère de Riemann.

La théorie des systèmes dynamiques a largement utilisé ces résultats pour étudier les ensembles de Julia associés à un polynôme, ainsi que l'ensemble de Mandelbrot : il est en effet possible dans ce cas de construire explicitement les transformations conformes dont l'existence est garantie par le théorème ; c'est ainsi, par exemple que l'on démontre que l'ensemble de Mandelbrot est connexe. L'image par ces transformations de points de la frontière des ensembles (qui sont donc des points du cercle unité) joue un rôle essentiel dans la théorie ; voir l'article anglais sur les arguments externes pour plus de détails. Ces constructions sont, au demeurant, proches des idées de Riemann, et relèvent de manière essentielle de la théorie du potentiel.

Les généralisations du théorème sont de deux sortes : d'abord, on dispose de résultats analogues dans le cas d'ouverts non simplement connexes du plan (mais on a vu que le petit nombre de transformations conformes en dimension supérieure interdit en revanche tout espoir de généralisation à ce cas) ; le plus simple de ces résultats est le théorème de Tsuji, caractérisant les applications conformes entre ouverts topologiquement isomorphes à un disque privé de son centre (les ouverts "doublement connexes"), et montrant qu'un tel ouvert est toujours conforme à une couronne circulaire. D'autre part, le problème du prolongement d'une telle application conforme au disque unité fermé s'est avéré redoutable ; on dispose par exemple du théorème de Carathéodory (en), qui montre qu'un tel prolongement continu existe si la frontière de U est une courbe de Jordan.