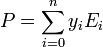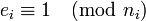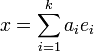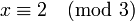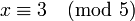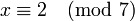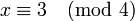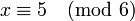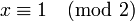Théorème des restes chinois - Définition

Système de congruences d'entiers

Théorème

Soient n₁, ..., n_k des entiers deux à deux premiers entre eux (ce qui veut dire pgcd (n_i , n_j) = 1 lorsque i ≠ j). Alors pour tous entiers a₁, ..., a_k, il existe un entier x, unique modulo et tel que

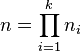
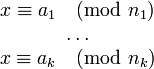
Une solution x peut être trouvée comme suit:

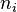
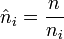
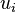
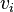
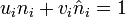
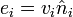
Pour chaque i, les entiers et sont premiers entre eux, et d'après le théorème de Bachet-Bézout, on peut trouver des entiers et tels que . Si on pose , alors nous avons

et

pour j ≠ i.

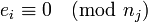
Une solution de ce système de congruences est par conséquent

Plus généralement, toutes les solutions x de ce système sont congrues modulo le produit n

Exemple

Le problème des soldats se réduit à

on obtient alors

• 
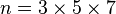
• n₁ = 3 et , or donc e₁ = 70
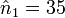
• n₂ = 5 et , or donc e₂ = 21
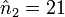
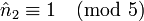
• n₃ = 7 et , or donc e₃ = 15

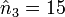
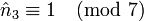
une solution pour x est alors

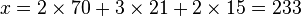
et les solutions sont tous les entiers congrus à 233 modulo 105, c'est-à-dire à 23 modulo 105.

Généralisation à des nombres non premiers entre eux

Quelquefois, les systèmes de congruences peuvent être résolus même si les ne sont pas premiers entre eux deux à deux. Le critère précis est le suivant : une solution x existe si et seulement si pour tous i et j. Toutes les solutions x sont congrues modulo le PPCM des n_i .

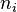
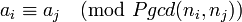
Exemple : résoudre le système

équivaut à résoudre le système

équivaut au système

• n₁ = 4 et , or donc e₁ = 9
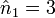
• n₂ = 3 et , or donc e₂ = 4

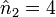
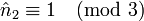
Une solution est donc ou tout autre nombre congru à 11 modulo 12

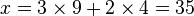
La méthode des substitutions successives peut souvent fournir les solutions des systèmes de congruences, même lorsque les modules ne sont pas premiers entre eux deux à deux.

Interprétation mécanique

La résolution du système suivant :

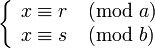
d'inconnue x passe par le calcul du PPCM de a et b.

Ce problème mathématique est une modélisation d'un problème sur des engrenages: une roue dentée comportant a dents s'engrène dans une tringle horizontale. Combien de dents doivent passer pour que sa r-ième dent vienne en coïncidence avec la s-ième dent d'une autre roue dentée comportant elle b dents ?

Le PPCM des deux nombres a et b est ce qui permet de comprendre le comportement périodique de ce système : c'est le nombre de dents séparant deux contacts de même congruence. On peut donc trouver la solution , s'il y en a une, dans l'intervalle [1,PPCM(a,b)]. Il y a une solution si PGCD(a , b) divise r - s.

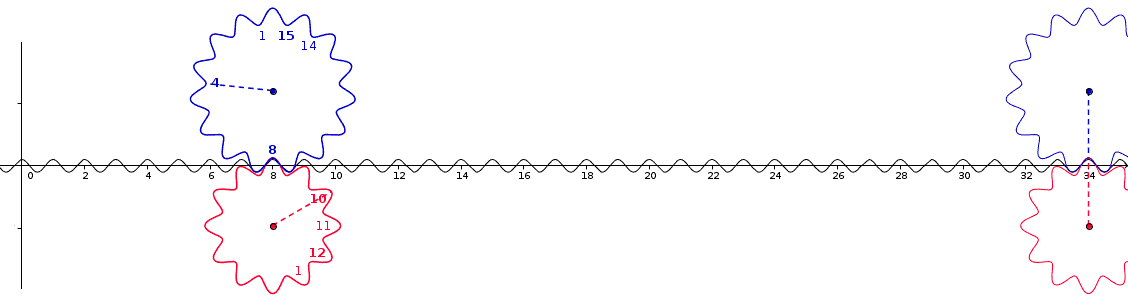
On peut comprendre simplement pourquoi le calcul sur des roues dentées fait intervenir de l'arithmétique modulaire, en remarquant que l'ensemble des dents d'une roue en comptant n peut être paramétré par l'ensemble des racines nèmes de l'unité, qui a une structure de groupe naturellement isomorphe à celle de Z/nZ.

Utilisations

Le théorème des restes chinois est utilisé en particulier dans l'algorithme RSA en cryptographie, il intervient aussi dans L'algorithme de Silver-Pohlig-Hellman (en) pour le calcul du logarithme discret.

Il permet de représenter de grands nombres entiers comme n-uplets de restes de divisions euclidiennes. Sous cette forme, des opérations comme l'addition ou la multiplication peuvent se faire en parallèle en temps constant (pas de propagation de retenue). Par contre, la comparaison ou la division ne sont pas triviales.

Exemple des polynômes

Un cas fréquent illustrant le paragraphe précédent est donné par l'anneau des polynômes. Si x₀, x₁, ..., x_n sont n+1 éléments de distincts deux à deux, alors on peut prendre U_i = X - x_i . Les polynômes U_i sont premiers entre eux deux à deux, et le théorème des restes chinois s'applique. On prend pour E_i les polynômes interpolateurs de Lagrange, définis par : .

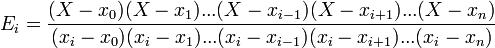
Pour j différent de i, E_i est divisible par U_j , de sorte que E_i ≡ 0 modulo U_j . Par ailleurs, modulo U_i , X ≡ x_i , de sorte que E_i ≡ 1 modulo U_i .

Dire qu'un polynôme P est tel que P(x_i) = y_i pour tout i, est équivalent à dire que P ≡ y_i modulo U_i . Un tel polynôme P est donné par , ce qu'on peut vérifier par un calcul direct.