Théorèmes énergétiques - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Les théorèmes énergétiques permettant de poser un problème de mécanique sous forme d'un problème de minimisation, et donc d'utiliser toutes les méthodes existantes pour ce genre de problèmes. Il y a deux théorèmes énergétiques, l'un est beaucoup plus connu que l'autre, il s'agit du théorème de l'énergie potentielle. Le second théorème est similaire au premier, la seule différence étant que dans un cas on parle de l'énergie potentielle et dans l'autre de l'énergie complémentaire.
Théorème de l'énergie potentielle
Le champ de déplacement solution d'un problème statique de mécanique des milieux continus minimise l'énergie potentielle du milieu.
Exemples
Soit un solide sur un plan sans frottement, relié à un ressort de raideur 'k' et soumis à une force 'F'.
On repère la position de référence du solide par 'x=0', et on suppose que cette position coïncide avec la position de repos (ou longueur à vide) du ressort. On note 'T' la tension du ressort.
Résolution en utilisant le théorème de l'énergie potentielle
L'énergie potentielle du système s'écrit :
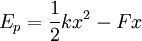
La minimisation de cette énergie donne :
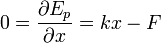
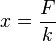
Résolution par l'énergie complémentaire
L'énergie complémentaire du système s'écrit :
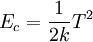
Ici comme l'on se doit de chercher 'T' dans l'espace des champs admissibles, on a du fait de l'effort 'F' imposé, 'T' = '-F', et comme on a un problème à 1 ddl, on a la solution.
Théorème de l'énergie complémentaire
Le champ de déplacement solution d'un problème statique de mécanique des milieux continus minimise l'énergie complémentaire du milieu
Démonstrations
À partir de l'erreur en relation de comportement
Établissement de l'expression de l'énergie potentielle et de l'énergie complémentaire
Soit e l'erreur en relation de comportement. Partons de l'expression de e2. On a :
![e^2\left(\underline{u},\underline{\underline{\sigma}}\right) = \frac{1}{2} \int_\Omega \operatorname{Tr}\left[\left(\underline{\underline{\sigma}} - \underline{\underline{\underline{\underline{K}}}}\cdot \underline{\underline{\varepsilon(u)}}\right) \cdot\underline{\underline{\underline{\underline{K}}}}^{-1} \cdot\left(\underline{\underline{\sigma}}- \underline{\underline{\underline{\underline{K}}}} \cdot\underline{\underline{\varepsilon(u)}}\right)\right] \mathrm d\Omega](https://static.techno-science.net/illustration/Definitions/autres/6/6237a61409a71fdef4722f670090bb0a_cdf52354ee35215a3c7d94a4733aa695.png)
![=\frac{1}{2}\left[ \int_\Omega \operatorname{Tr}\left(\underline{\underline{\sigma}}\cdot \underline{\underline{\underline{\underline{K}}}}^{-1} \cdot\underline{\underline{\sigma}}\right)\mathrm d\Omega + \int_\Omega \operatorname{Tr}\left(\underline{\underline{\underline{\underline{K}}}}\cdot \underline{\underline{\varepsilon}} \cdot\underline{\underline{\varepsilon}}\right) \mathrm d\Omega - 2 \int_\Omega \operatorname{Tr}\left(\underline{\underline{\sigma}}\cdot \underline{\underline{\varepsilon}}\right)\mathrm d\Omega \right]](https://static.techno-science.net/illustration/Definitions/autres/4/4f53af799c3d9107479357c50663bc3d_5a6f638b0037303cdb9547d5ebe6d127.png)
On applique alors la formule de Green :
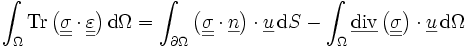
On peut séparer l'intégrale sur le bord de Ω en deux intégrales : une sur
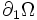
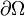
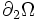
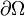
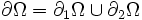
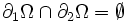
On obtient donc, en utilisant les équations d'équilibre et les conditions aux limites :
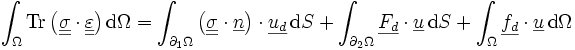
Soit
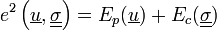
Avec :
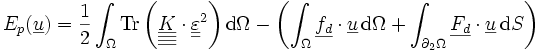
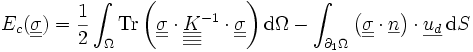
Étude des différents termes de ces expressions
Énergie potentielle
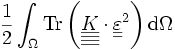
est l'énergie de déformation exprimée en déplacement. C'est l'analogue de l'énergie de déformation élastique d'un ressort
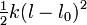
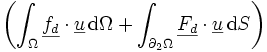
est le travail des efforts imposés (donc connues) dans le champ de déplacement inconnu. C'est une forme linéaire continue.
Énergie complémentaire
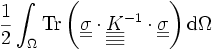
est l'énergie de déformation exprimée en contrainte, c'est l'analogue de l'énergie de déformation élastique d'un ressort exprimée en fonction de la force
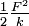
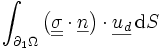
est le travail des efforts inconnus dans le champ de déplacement imposé (donc connu) Ep(u) ne dépendant que de u et des forces imposées. C'est une forme linéaire continue.
Démonstration des théorèmes énergétiques
Nous savons que la solution exacte est telle que
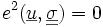
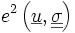
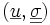
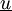
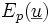
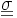
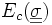
De plus nous sommes dans les hypothèses d'application du théorème de Stampacchia qui garantit l'existence et l'unicité des solutions de chacun de ces problèmes de minimisation.
De plus le déplacement et la contrainte étant liés par la relation de comportement, on peut choisir de minimiser l'une ou l'autre de ces énergies pour obtenir le couple solution.
À partir de l'équation d'équilibre local
On peut faire des formulations variationnelles en déplacement v CA0 (ci dessous) ou contrainte to CA 0 et obtenir a(u,v)=l(v) ou a(sigma, to)=l(to) équations à résoudre.
Énergie potentielle, formulation en déplacement
on cherche
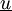
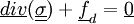
vérifiant la relation de comportement
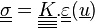
On multiplie par un champ cinématiquement admissible à zéro
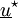
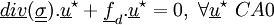
Un intégration donne :
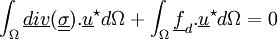
La formule de Green permet d'arriver à :
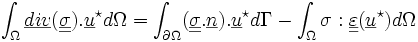
Soit:
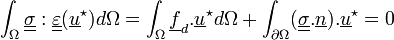
On décompose le bord du domaine en deux: lieux à efforts imposés
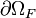
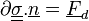
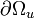
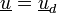
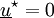
On obtient alors :
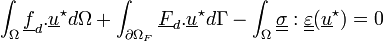
En utilisant la relation de comportement, on aboutit au problème suivant :
trouver
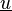
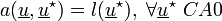
Avec
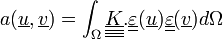
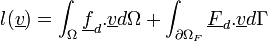
On peut alors vérifier que l'on est dans le cadre d'application des théorèmes de Lax-Milgram et de Stampacchia, qui assurent d'une part, l'existence et l'unicité de la solution, d'autre par l'équivalence de ce problème au problème de minimisation de la fonctionnelle
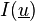
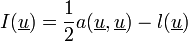
Cette fonctionnelle n'est autre que l'énergie potentielle.
Énergie complémentaire, formulation en contrainte
L'établissement du théorème de l'énergie complémentaire se fait de la même façon, mais en posant une formulation variationnelle en contrainte, pour cela il faut partir de la relation de comportement et la multiplier par un champ de contraintes statiquement admissible à zéro.